Лекция 3
7. (Интегральный признак Коши) Пусть f монотонная
невозрастающая неотрицательная функция на ![]()
![]() . Ряд
. Ряд ![]() и интеграл
и интеграл ![]() одновременно сходятся или
расходятся, и если сходятся, то
одновременно сходятся или
расходятся, и если сходятся, то ![]()
![]() .
.
Доказательство
![]()
![]()
![]() .
.
Следствие 1
Ряд ![]() сходится при a>1 и расходится при a<1.
сходится при a>1 и расходится при a<1.
8. (Признак Куммера) Пусть ![]() ряд со строго положительными
членами и bk, kÎN,
последовательность со строго положительными членами. Пусть
ряд со строго положительными
членами и bk, kÎN,
последовательность со строго положительными членами. Пусть 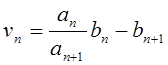 : 1) Если
: 1) Если ![]() , то ряд
, то ряд ![]() сходится.
сходится.
2) Если ![]() и
ряд
и
ряд ![]() расходится, то и ряд
расходится, то и ряд ![]() расходится.
расходится.
Доказательство
1*) ![]()
![]() . Значит ряд
. Значит ряд ![]() сходится, и ряд
сходится, и ряд ![]() тоже сходится.
тоже сходится.
2*) Если ![]() .
. 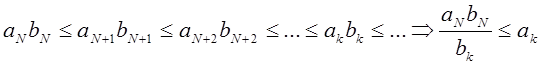 . Тогда из расходимости ряда
. Тогда из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда 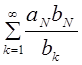 и расходимоть ряда
и расходимоть ряда ![]() .
.
Следствие 2
Пусть ![]() ряд со строго положительными
членами и bn – строго положительная последовательность. Если
ряд со строго положительными
членами и bn – строго положительная последовательность. Если 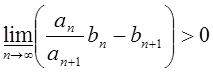 , то ряд
, то ряд ![]() сходится.
сходится. 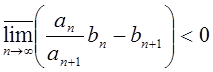 и ряд
и ряд ![]() расходится, то и ряд
расходится, то и ряд ![]() расходится.
расходится.
9. (Признак Раабе) Пусть ![]() ряд со строго положительными
членами. Пусть
ряд со строго положительными
членами. Пусть  . Если r>1, то ряд
. Если r>1, то ряд ![]() сходится, а если r<1, то
расходится.
сходится, а если r<1, то
расходится.
Доказательство
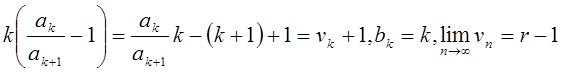 .
.
10. (Признак Гаусса) Пусть ![]() ряд со строго положитеьными
членами и
ряд со строго положитеьными
членами и 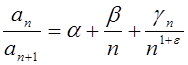 , где a,b,e – числа, e>0, а gn
– ограниченная последовательность Þ
при a>1 или a=1, b>1
ряд
, где a,b,e – числа, e>0, а gn
– ограниченная последовательность Þ
при a>1 или a=1, b>1
ряд ![]() сходится, а при a<1 или a=1,при b£1, ряд
сходится, а при a<1 или a=1,при b£1, ряд ![]() расходится.
расходится.
Доказательство
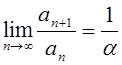 по признаку Даламбера при
по признаку Даламбера при ![]() ряд сходится, а при
ряд сходится, а при ![]() расходится.
расходится.
1*) a=1 Þ 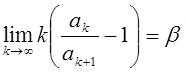 по признаку
Раабе при b>1 ряд сходится, а при b<1 расходится.
по признаку
Раабе при b>1 ряд сходится, а при b<1 расходится.
2*) a=1, b=1. Пусть
![]() . Ряд
. Ряд ![]() расходится по интегральному
признаку Коши.
расходится по интегральному
признаку Коши. 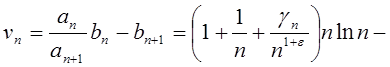
![]()
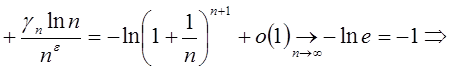 ряд
расходится.
ряд
расходится.
Знакопеременные ряды
1.(Признак Лейбница) Пусть ![]() ряд действительных чисел со
знакопеременными членами (то есть ak – знакочередующаяся
последовательность, все ak с нечетными k одного знака, а все ak
с четными k другого) и | ak | – невозрастающая, стремящаяся к 0
последовательность. Тогда это ряд Лейбница, он сходится и
ряд действительных чисел со
знакопеременными членами (то есть ak – знакочередующаяся
последовательность, все ak с нечетными k одного знака, а все ak
с четными k другого) и | ak | – невозрастающая, стремящаяся к 0
последовательность. Тогда это ряд Лейбница, он сходится и ![]() .
.
Доказательство
Пусть ak с нечетными k неотрицательны, а ak с
четными k неположительны Þ ![]() Þ
S2n неубывающая последовательность.
Þ
S2n неубывающая последовательность. ![]() Þ S2n+1 невозрастающая
последовательность. И
Þ S2n+1 невозрастающая
последовательность. И ![]()
![]() , S2n
– сходится,
, S2n
– сходится, ![]() , S2n+1
– сходится.
, S2n+1
– сходится. ![]() .
.
Рассмотрим ![]() .
.
С другой стороны ![]() .
.
Рассмотрим ![]()
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.