Метод Абеля. Функциональные ряды. Свойства равномерной сходимости

Лекция 8-9

Теорема 1

Метод Абеля линеен и вполне регулярен.

Доказательство

Докажем, что если , то ряд суммируется методом Абеля к +¥. .

1) При некотором , ряд  Þ по признаку сравнения при  имеем  при  имеем  ряд суммируется методом Абеля к +¥.

2) При ", ряд  сходится Þ его члены стремятся к 0 и имеем: .

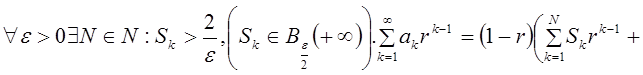
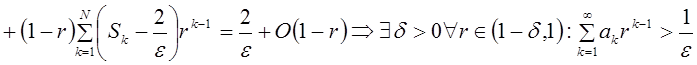  Þ ряд суммируется методом Абеля к +¥.

Пример 1

1)

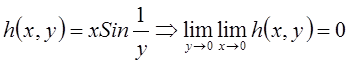
2) .

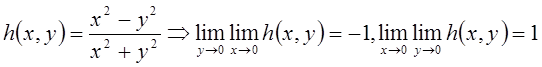Теорема 2 (критерий Гордона)

Пусть h(x,y) функция из  в R(C). В Х $ база Б, а в Y $ база Д. Пусть  для  и  для . Тогда оба повторных предела  и  существуют и равны Û .

Доказательство

1*) Докажем необходимость. Пусть . Возьмем " e>0. Найдем . Возьмем "хÎB₁ и найдем . Найдем  . Положим  .

2*) Докажем достаточность.

А) Докажем, что . Возьмем " e>0 и найдем  . Возьмем  и оценим .   .  .

Найдем . Найдем  . Пусть  . Пусть .

Б) Докажем, что . Возьмем " e>0 и Д  . . Найдем э. Фиксируем  и соответственно . Найдем  для  .

Пример 1

Двойной ряд  . , когда  и  существуют и равны. По критерию Гордона должны существовать  и . Оба повторных предела существуют и равны Û  .

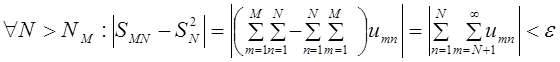Функциональные ряды

Определение 1

Функциональная последовательность (ряд) на множестве Е – это последовательность  (ряд ) определенных на Е функций.

Определение 2

Функциональная последовательность (ряд) сходится в точке х₀, если все функции последовательности  (ряда ) определены в точке х₀, и сходится числовая последовательность  ( числовой ряд ).

Предел функциональной последовательности (сумма функционального ряда) в точке х₀ – это  .

Определение 3

Функциональная последовательность (ряд) сходится на множестве Е, если она (он) сходится в " точке множества Е.

Определение 4

Функциональная последовательность  сходится равномерно на множестве Е к функции f, если все f_k и f определены на Е и  , или .

Определение 5

Функциональный ряд  сходится равномерно на Е к функции S(x) если f_k(x) и S(x) определены на Е, и последовательность частичных сумм  сходится равномерно к S(x) на Е.

Определение 6

Функциональная последовательность (ряд) сходится равномерно на множестве Е, если $ функция на Е, к которой последовательность (последовательность частичных сумм ряда) сходится равномерно.

Свойства равномерной сходимости

1) Если последовательность  сходится равномерно на Е к f Þ она сходится равномерно на " подмножестве.

2) (линейность) Если функциональная последовательность  сходится равномерно на Е (к f(х)) Þ для " a функциональная последовательность  сходится равномерно на Е (к a f(х)); если  и  сходится раномерно на Е (к f(х) и к g(х) соответственно) Þ функциональная последовательность  сходится равномерно на Е (к f(x)+g(x)).

Доказательство

.

3) Если функциональная последовательность  сходится равномерно на Е (к f(x)), а g(x) ограниченная функция на Е Þ  сходится равномерно на Е (к f(x)g(x)).

Доказательство

.