Методичні рекомендації та завдання до контрольної роботи з курсу “Математичне програмування”

НАЦІОНАЛЬНИЙ БАНК УКРАЇНИ

УНІВЕРСИТЕТ БАНКІВСЬКОЇ СПРАВИ

ХАРКІВСЬКИЙ ІНСТИТУТ БАНКІВСЬКОЇ СПРАВИ

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

та завдання до контрольної роботи

з курсу“Математичне програмування”

для студентів ІІ курсу заочної форми навчання

 усіх спеціальностей

Харків 2007

 І. Загальні пояснення та рекомендації

до виконання контрольної роботи.

          Контрольна робота містить завдання з курсу:  “Математичне програмування”.

Необхідно з самого початку вірно встановити свій варіант (від 1 до 10), який відповідає останній цифрі номера за журналом групи.

          Основні вимоги до виконання контрольної роботи:

·  самостійність виконання;

·  своєчасність надіслання роботи;

·  відповідність номера варіанта (в противному разі робота буде повернена на повторне виконання);

·  робота повинна бути виконана повністю;

·  завдання треба розташовувати по порядку за номерами, що вказані в контрольній роботі, із зберіганням нумерації;

·  кожне завдання необхідно оформити за такою схемою: умова завдання (переписати у відповідності до свого варіанту); розв’язання задач (має бути обгрунтованим, з наведенням формул, назв відповідних теорем, відомих фактів, якими користувалися); відповідь (повна);

·  роботу треба виконати в окремому зошиті з полями для зауважень викладача, інтервалами між рядками, без скорочень, розбірливим почерком;

·  наприкінці роботи наводиться список літератури, ставиться дата її виконання, підпис студента, залишається місце для рецензії.

Перед виконанням завдань контрольної роботи необхідно детально вивчити методичні вказівки (див. розділи ІІІ, IV), які містять стислий виклад основних теоретичних відомостей, формули, алгоритми, приклади, список літератури до кожного завдання і мають метою допомогти студенту самостійно оволодіти матеріалом і навичками розв’язання задач.

Студенти, які не здали контрольну роботу до початку сесії, не можуть бути допущеними до складання екзамену (заліку). Контрольна робота, що вважається викладачем задовільною, оцінюється як “зарахована”. Якщо в роботі допущені помилки, не всі відповіді розкривають зміст питань, вона не зараховується і повертається студентові для доопрацювання (у тому ж зошиті). Роботи, що виконані несамостійно, неохайно, нерозбірливим почерком, а також не за встановленим варіантом, повертаються без перевірки.

Список рекомендованої літератури:

1.  Акулич И.Л., Математическое программирование в примерах и задачах. – М.: Высш. шк.,1986. – 319 с.

2.  Барковський В.В., Барковська Н.В., Лопатін О.К. Математика для економістів. Теорія ймовірностей та математична статистика. – К.: Національна академія управління, 1999.

3.  Красс М.С., Чупрінов Б.П. Основы математики и ее приложения в экономическом образовании. – М.: Дело, 2001–688 с.

4.  Гетманцев В.Д. Лінійна алгебра і лінійне програмування. – К.: Либідь, 2001. – 256 с.

5.  Калихман И.С. Сборник задач по математическому программированию. – М.: Высш. шк., 1975.

6.  Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Наука, 1965 – 275 с.

ІІ. ЗАВДАННЯ КОНТРОЛЬНОЇ РОБОТИ

(n – номер варіанта (від 1 до 10), відповідає останній цифрі номера за журналом)

Завдання № 1

Розв’язати задачу лінійного програмування графічним методом:

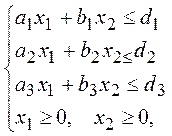
F=c₀+c₁x₁+ c₂x₂→max.

Значення коефіцієнтів взяти, відповідно до номера варіанта, з таблиці:

Номер варіанта	a1	b1	d1	a2	b2	d2	a3	b3	d3	c0	c1	c2
1	7	5	35	4	7	28	1	6	18	-2	3	1
2	4	3	24	6	7	42	1	3	15	0	2	1
3	1	2	10	1	1	6	3	1	12	5	3	2
4	2	1	16	1	1	11	1	3	27	0	1	2
5	1	3	18	2	1	18	1	1	10	0	2	3
6	1	6	18	4	7	28	7	5	35	2	4	1
7	1	3	15	4	3	24	6	7	42	-3	1	5
8	3	1	12	1	2	10	1	1	6	-2	1	5
9	1	3	27	2	1	16	1	1	11	0	4	3
10	1	1	10	2	1	18	1	3	18	1	3	2

Завдання № 2.не робим

            Розв’язати попередню задачу симплекс-методом.

Завдання № 3.

Розв’язати транспортну задачу лінійного програмування.

На чотири бази А₁, А₂, А₃, А₄ поступив однорідний вантаж відповідно у кількості а₁, а₂, а₃, а₄. Отриманий вантаж треба перевезти у п’ять пунктів призначення В₁, В₂, В₃, В₄, В₅ у кількості відповідно в₁, в₂, в₃, в₄, в₅. Вартість перевезення одиниці вантажу C_ij від і-го постачальника до j-го споживача вказано в таблиці:

Поста- чальник	Споживач					Наявність вантажу аі
	В1	В2	В3	В4	В5
А1	7+n	19	21-n	9	9+ n	85
А2	6	20- n	20	8+ n	7	220
А3	18- n	8	7+ n	20	21- n	105
А4	19	6+ n	8	21- n	17	200
Потреба у вантажі вj	70+10n	80+5n	60+5n	190-10n	210-10n	610

          Скласти план перевезення вантажу від постачальників до споживачів, що має мінімальну вартість перевезення.

ІІІ. МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ

1.  Графічний метод розв’язання задачі лінійного програмування

Література: [1], 26-27; [5], 42-52; [6, 151-163].

Алгоритм.

1)  Побудувати многокутник розв’язків системи обмежень як перетин півплощин, що задані нерівностями системи.

2)  Знайти градієнт цільової функції gradF.

3)  Побудувати лінію рівня (пряму, перпендикулярну gradF) і пересувати її в напряму gradF до перетину з останньою точкою многокутника розв’язків.

4)  Обчислити координати знайденої точки та значення цільової функції в цій точці.

Приклад. Розв’язати графічним методом задачу лінійного програмування:

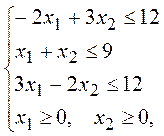
F=5+2x₁+4x₂→max.

Розв’язання. Зобразимо на площині систему координат Оx₁x₂ і побудуємо граничні прямі області допустимих розв’язків:  -2x₁+3x₂=12  (1), x₁ +x₂=9  (2), 3x₁-2x₂=12  (3),  x₁=0,  x₂=0. Область припустимих значень визначається многокутником ОАВСД:

 

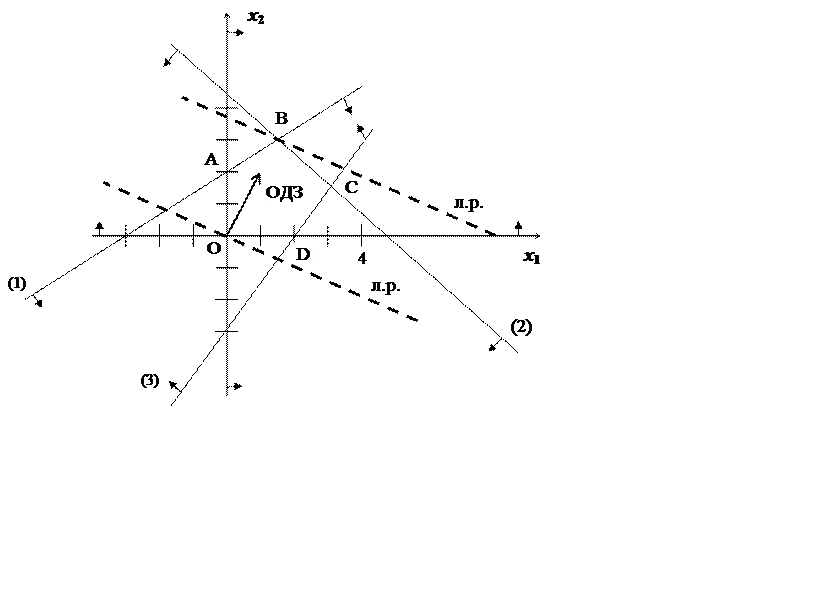Знайдемо gradF=(2;4), побудуємо цей вектор так, щоб його початок знаходився у початку координат. У напрямі вектора gradF переміщуємо лінію рівня (вона перпендикулярна gradF) до останньої точки перетину з многокутником (це можна зробити за допомогою лінійки та трикутника), в результаті одержуємо точку В, яка є точкою перетину прямих (1) і (2). Розв’язавши систему рівнянь (1) і(2), знаходимо координати точки В: x₁=3, x₂=6 (перевірте). Це і буде оптимальний розв’язок даної задачі, якому відповідає максимальне значення цільової функції F_max=5+2∙3+4∙6=35.

  Відповідь: x₁=3, x₂=6, F_max=35.

2.  Симплексний метод

Література: [1], 49-55; [3], 367–379; [4], 151–182; [6], 164–208.