Методичні рекомендації та завдання до контрольної роботи з курсу “Математичне програмування”, страница 3

3. Серед коефіцієнтів лінійної функції F₁ оберемо додатній (краще менший). В нашому випадку це 2.

4. Для обраного коефіцієнта (2) і відповідного становища (назвемо його дозволяючим) обчислемо відношення вільних членів до коефіцієнтів при відповідних вільних змінній в системі обмежень (табл. 2). Найменше  з цих відношень визначає дозволяючий елемент (a=3)

5. Обчислемо l=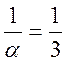. Помножемо  на l елементи дозволяючого рядка і на “–l” елементи дозволяючого стовпця.

6. В дозволяючому рядку обведемо кружками всі верхні числа, в дозволяючому стовпці – всі нижні (окрім a та l).

7. Для елементів, які  не належать до дозволяючого рядка та стовпця, в нижній трикутник запишемо добуток обведених кружками відповідних чисел.

8. Побудуємо нову таблицю (табл. 3). Зробимо обмін змінних (х₅ стає вільною х₂ – базовою), на який вказує дозволяючий елемент a. Елементи дозволяючого рядка та дозволяючого стовпця – це числа з нижніх трикутників відповідного рядка та стовпця попередньої таблиці. Ві інші елементи – це  сума чисел, які записані в верхньому та нижньому трикутниках попередньої таблиці.

9. Процедуру заповнення таблиць продовжимо доти, доки всі коефіцієнти лінійної функції F₁ (за винятком вільного числа) не стануть від’ємними (або нулями) (табл. 4).

Відповідь: х₁=4; х₂=2; F_max=17.

Табл. 1                                                                         Табл. 2

	b	x1	x2			b	x1	x2
10   x3	10	2	1		x3	10	2	1
x4	10	1	2		x4	10	1	2
x5	16		3		x5	16		3
F1	-1	3	2		F1	-1	3	2

Табл. 3                                                                         Табл. 4

	b	x1	x2			b	x1	x2
x3	4				x3	4
x4					x4
x5					x5	2
F1					F1	-17

3.  Транспортна задача

Література: , 140-154;  , 85-99.

Загальна методика розв’язування транспортної задачі

1.  Знаходимо перший опорний план (див. нижче алгоритм №1).

2.  Перевіряємо опорний план на оптимальність. Якщо план не оптимальний, поліпшуємо його до оптимального (див. алгоритм № 2).

Зауваження. Перед вивченням алгоритмів №№ 1,2 необхідно уважно розглянути позначення в умові транспортної задачі (див. умову останньої задачі у контрольній роботі).

Алгоритм №1.

(алгоритм знаходження опорного плану методом мінімуму по рядку).

1.  У першому рядку знаходимо клітину з найменшим С_1l. Розглянемо цю клітину (або будь-яку з них, якщо їх декілька).

2.  Завантажуємо обрану клітину максимально. Можливі три випадки:

а) а₁<b_l.  Завантажуємо клітину кількістю вантажу x_1l=а₁ (тим самим весь вантаж у першого постачальника вивезений, а потреба у вантажі споживача В_l :  b_l′=b_l-a₁). Переходимо до наступного рядка (розглядаючи його як перший);

б) а₁>b_l.  Завантажуємо клітину кількістю вантажу x_1l=b_l (тим самим потреба споживача b_l цілком задоволена, у постачальника А₁ залишилося вантажу а₁′=а₁-b_l). Переходимо до слідуючої за мінімумом С_ll  клітини першого рядка;

в) а₁=b_l.  Завантажуємо клітину кількістю вантажу x_ll=а₁-b_l (тим самим весь вантаж у постачальника А₁ вивезений, потреба споживача b_l цілком задоволена). Наступну за мінімумом С_1l клітину першого рядка завантажуємо фіктивним вантажем, рівним нулю, переходимо до наступного рядка (який далі розглядаємо як перший). Фіктивне завантаження не ставиться в повністю завантажений стовпець і в останньому рядку.

Зауваження. Існують інші алгоритми побудови опорного плану ( див. , с. 140-143).

Алгоритм №2

(алгоритм методу потенціалів)

1.  За опорним планом знаходимо потенціали рядків і стовпців за правилом U₁=0, U_k+V_l=C_kl для завантажених клітин.

2.  Знаходимо потенціали незавантажених клітин за формулою

p_kl=U_k+V_l-Ck_l.

Можливі два випадки:

а) усі p_kl≤0; у цьому випадку опорний план є оптимальним; задача розв’язана;

б) є потенціал p_kl>0; переходимо до п. 3.

3.  Беремо незавантажену клітину з найбільшим додатнім потенціалом (або будь-яку з них, якщо таких клітин декілька) і приєднуємо її до клітин опорного плану.

4.  Будуємо цикл, утворений обраною клітиною з клітинами опорного плану, з’єднуючи ці клітини вертикальними та горизонтальними відрізками.