Другие предметы \ Математическое программирование

Методичні рекомендації та завдання до контрольної роботи з курсу “Математичне програмування”, страница 4

5. Нумеруємо клітини циклу, починаючи від приєднаної до опорного плану (ця клітина обов'язково потрапляє в цикл), рухаючись уздовж циклу. Клітини з непарними номерами утворять непарний півцикл, із парними – парний півцикл.

6. Серед завантажень клітин парного півциклу знаходимо найменше завантаження x_min.

7. Робимо перенос по циклу: із завантажень клітин парного півциклу віднімаємо x_min, до завантажень клітин непарного півциклу додаємо x_min. Клітину парного півциклу, у якої завантаження стало рівним нулю (або будь-яку з них, якщо таких клітин декілька), викидаємо з множини завантажених клітин (тим самим розриваємо цикл) і переходимо до п. 1.

Розв’язання транспортної задачі продемонструємо на прикладі, дані яких наведені в табл. 1.

Табл. 1

Постачальник	Споживач					Наявність вантажу
Постачальник	В₁	В₂	В₃	В₄	В₅	Наявність вантажу
А₁	8	7	9	5	11	120
А₂	4	12	14	8	9	150
А₃	7	10	19	4	11	180
А₄	4	12	7	13	10	250
Потреба у вантажі	110	195	165	100	130	700

Змінимо транспортну матрицю, для цього введемо рядок для потенціалів V₁ і стовпчик для потенціалів U_k. Кожну клітину розділимо навпіл діагоналлю, над якою будемо писати C_kl, а під діагоналлю - x_kl. Замість першого стовпчика поставимо стовпчик наявності вантажу а_k, а замість першого рядка - потреби b_l (табл. 2).

Табл. 2

b_l a_k	110	195	165	100	130
120	8	7 20	9	5 100	11	0
150	4 110	12	14	8	9 40	4
180	7	10 15	9 165	4	11	3
250	9	12 160	7	13	10 90	5
	0	7	6	5	5	U_k V_l

Будуємо опорний план методом мінімуму по рядку. У першому рядку мінімальне С_1l дорівнює С₁₄=5 (клітина А₁В₁). Завантажуємо клітину, вважаючи х₁₄=100. У А₁ залишилося 20 одиниць вантажу. Переходимо до слідуючої клітини за мінімумом С_1l - це клітина А₁В₂, де С₁₂=7. Завантажуємо її х₁₂=20 і переходимо до другого рядка, де minC_2l=C₂₁=4. Клітину А₂В₁ завантажуємо х₂₁=110. Переходимо до клітини А₂В₅:С₂₅=9 (у рядку є клітина А₂В₄, у якій С₂₄=8<9, але потреба В₄ уже задоволена). Завантажуємо х₂₄=40. Переходимо до третього рядка. Мінімальне С_3l по не повністю завантажених стовпцях дорівнює С₃₃=9. Завантажуємо клітину А₃В₃: х₃₃=165 і клітину А₃В₂ х₃₂=15. Заповнимо далі четвертий рядок: х₄₅=90, х₄₂=160. Кількість завантажених клітин 8=m+n-1 де m=4 - кількість постачальників, n=5 - кількість споживачів (це входить в умову того, що отриманий план - опорний) (див. табл. 2).

Перевіряємо отриманий план на оптимальність. Для цього знаходимо потенціали рядків і стовпчиків:

U₁=0, V₂=7 (тому що U₁+V₂=C₁₂=7) тощо (див. табл. 2).

Знаходимо потенціали незавантажених клітин за формулою p_kl=U_k+V_l-C_kl: р₁₁== -8, р₃₄= -3 тощо (повністю обчислення зробіть самостійно).

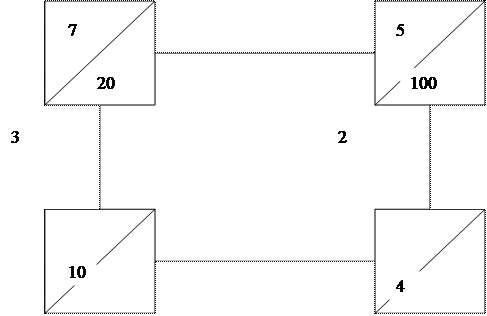
Серед потенціалів незавантажених клітин є додатні (перевірте), тому отриманий план не є оптимальним. Серед додатних потенціалів вибираємо найбільший: р₃₄=р₄₃=4. Беремо, наприклад, клітину А₃В₄ і приєднуємо її до клітин опорного плану. Знаходимо цикл (починаючи з клітини А₃В₄): А₃В₄-А₁В₄-А₁В₂-А₃В₂. Нумеруємо клітини циклу, починаючи з клітини А₃В₄

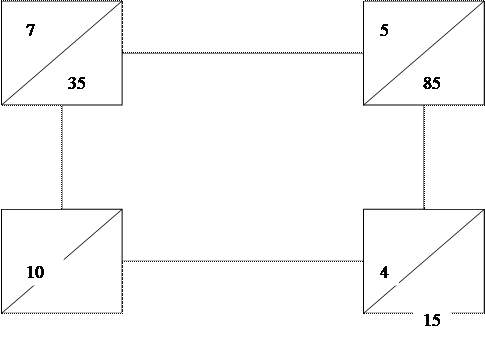
(рис. 1). Серед завантажень клітин парного півциклу знаходимо x_min=15 і робимо перенос по циклу: віднімаємо її з завантажень парного півциклу і додаємо до завантажень клітин непарного півциклу. Клітину А₃В₂ виводимо з множини завантажених клітин (рис. 2).

Рис. 1 Рис. 2

Одержуємо другий опорний план, який знову перевіряємо на оптимальність. Цей процес продовжуємо, поки потенціали всіх незавантажених клітин не стануть недодатніми (зробіть самостійно). Оптимальний план приведено в таблиці 3.

Табл. 3