Для розв’язання задачі лінійного програмування симплекс-методом треба перевести обмеження-нерівності системи в обмеження-рівняння. Для цього в кожному обмеженні-нерівності треба до меншої частини додати (свою для кожної нерівності) змінну, рівну різниці більшої і меншої частини кожної з нерівностей. Крім того, замість цільової функції F, яку треба максимізувати, вводять функцію F1= - F і шукають розв’язок системи обмежень, який мінімізує функцію F1.
Алгоритм симплекс-методу.
1. Знаходимо перший опорний план (перший припустимий базисний розв’язок). Виражаємо базисні змінні і цільову функцію через вільні змінні.
2. Перевіряємо умову досягнення оптимального розв’язку: якщо всі коефіцієнти при вільних змінних у виразі цільової функції через вільні змінні невід’ємні, то отриманий базисний розв’язок – оптимальний.
Розглядаємо коефіцієнти при вільних змінних у виразі цільової функції через вільні змінні.
Можливі два випадки:
а) серед цих коефіцієнтів немає від’ємних; у цьому випадку задача розв’язана, базисний розв’язок (отриманий при вільних змінних, що дорівнюють нулю) оптимальний;
б) серед коефіцієнтів є від’ємні; переходимо до п. 3.
3. Вибираємо вільну змінну, що має у виразі для цільової функції найбільший по модулю від’ємний коефіцієнт (або будь-яку з них, якщо таких змінних декілька).
4. Розглядаємо систему обмежень. Можливі два випадки:
а) у всіх обмеженнях коефіцієнти при обраній вільній змінній невід’ємні; у цьому випадку оптимального рішення не існує (min F=-∞);
б) є обмеження, що мають від’ємні коефіцієнти при обраній вільній змінній; у цьому випадку переходимо до п. 5.
5. Розглядаємо обмеження з від’ємними коефіцієнтами при обраній вільній змінній. Для кожного з них обчислюємо відношення вільного члена до коефіцієнта з протилежним знаком при обраній вільній змінній (знаходячи тим самим значення, до якого можна збільшити обрану вільну змінну при всіх інших вільних змінних, що дорівнюють нулю, так, щоб змінна, яка стоїть в лівій частині, залишалася невід’ємною).
6. Знаходимо серед цих відношень найменше і беремо обмеження, у якому досягається це найменше значення (або будь-яке з таких обмежень, якщо таких обмежень декілька); тим самим знаходимо найбільше значення, до якого можна збільшувати обрану вільну змінну при інших вільних змінних, рівних нулю, так, щоб усі змінні були невід’ємні.
Виражаємо вільну змінну з обраного обмеження, переводячи тим самим її в базисні змінні, а колишню базисну змінну, визначену обраним обмеженням, переводимо у вільні змінні. Одержуємо новий набір вільних і базисних змінних і переходимо до п. 1.
Приклад. Розв’язати симплекс-методом задачу лінійного програмування:
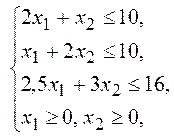
F=1+3x1+2x2→max.
Розв’язання. Перетворимо систему обмежень та цільову функцію так, щоб можна було застосовувати алгоритм симплекс-методу. Одержуємо задачу:
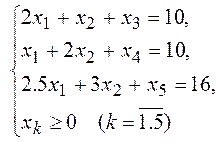(1)
F1=-1-3x1-2x2→ min. (2)
За базисні змінні приймемо х3, х4, х5, за вільні - х1, х2 . Виразимо базисні змінні через вільні. Система (1) прийме вигляд
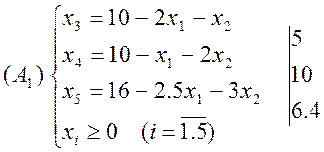
Цільова функція
F1 уже виражена через вільні змінні. Поклавши в (1) вільні
змінні х1=х2=0, одержуємо базисний
розв’язок 
=(0, 0, 10, 10, 16), що є припустимим
(тому що усі хk≥0). Цільова функція на цьому розв’язку: F1()=-1. Оскільки в (2)
коефіцієнти при х1 і х2 від’ємні, то х1
– неоптимальний розв’язок.
Обираємо змінну х1 (тому що 3>2). Розглянемо систему (1). У кожному з обмежень коефіцієнт при х1 від’ємний. Розглянемо в кожному обмеженні відношення вільного члена до коефіцієнта при х1 з протилежним знаком. У першому обмеженні це відношення дорівнює 5, у другому - 10, у третьому - 6,4. Найменше з них досягається в першому обмеженні.
Знаходимо х1 із першої рівності:
.
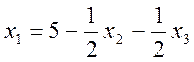Одержимо новий набір базисних (х1, х4, х5) і вільних (х2, х3) змінних.
Виразимо нові базисні змінні (х4, х5) і цільову функцію F1 через новий набір вільних змінних, підставляючи у вираз для кожного з них отриманий вираз для х1:
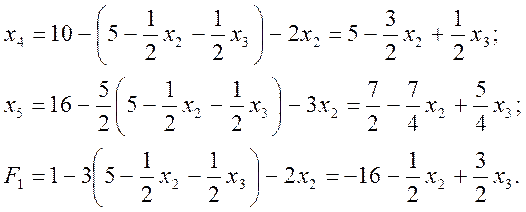
Таким чином, задача (1)-(2) прийме вигляд
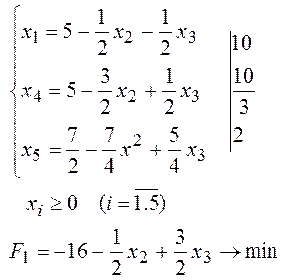
Одержали другий
базисний розв’язок: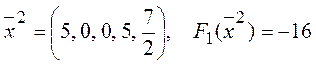 
. Цей розв’язок не є
оптимальним, тому що коефіцієнт при х2 у цільовій функції
від’ємний. Розглянемо систему обмежень. У першому обмеженні х2
можна збільшити до 10, у другому - до 10/3, у третьому - до 2. Виражаємо х2
з третього обмеження:
.
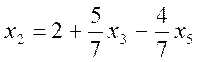Одержали новий набір базисних змінних (х1, х2, х4) і новий набір вільних змінних (х3, х5). Виразимо базисні змінні (х1, х4), що залишилися, і цільову функцію F1 через новий набір вільних змінних:
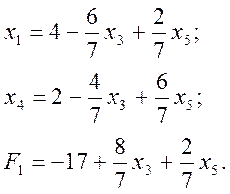
Таким чином, задача прийняла вигляд
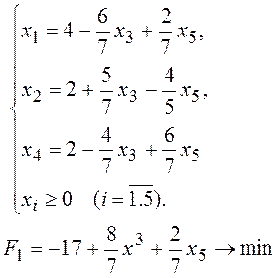
Одержали третій базисний розв’язок:
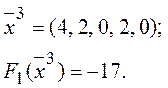
Через те, що всі коефіцієнти при вільних змінних у цільовій функції додатні, отриманий базисний розв’язок є оптимальним.
Отже, Fmax=17
і досягається на 
=(4, 2, 0, 2, 0).
Відповідь: x1=4, x2=2, Fmax=17.
Практична реалізація симплексного метода значно спрощується при вокористанні симплекс-таблиць. Розглянемо алгоритм для попереднього приклада.
Алгоритм табличного симплекс-метода.
1. Задачу лінійного програмування представимо в канонічній формі таким чином:
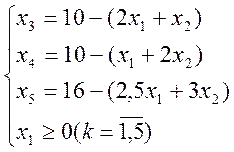
F1=1–(3x1+2x2)®min
2. Складемо вихідну симплекс-таблицю (Табл. 1) в якій число базисних (х3, х4, х5) і вільних (х1, х2) змінених визначається рангом матриці системи обмежень.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.