Качество: Основные понятия. Стандартизация, метрология, сертификация – основные инструменты обеспечения качества, страница 9

Для стрелочных приборов – это линейное dl и условное dα переменные конца стрелки, и чувствительность имеет размерность: 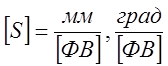, а если в делениях, то: .

Средняя чувствительность: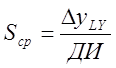

Для равномерной шкалы текущая чувствительность

Для неравномерной шкалы коэффициент  неравномерности

Относительная чувствительность 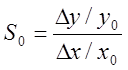, где х₀ ,y₀ – среднее или номинальные значения х,y.

Постоянная прибора 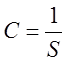 - величина, обратная чувствительности

Если выражена в делениях, то постоянная прибора равна цене деления: С=Ц,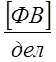

·  Порог чувствительности – наименьшая ФВ, дающая заметные отклонения .

·  Вариация (гистерезис) показаний – разность в показаниях СИ в данной точке значений ФВ в случае возрастания и убывания измеряемой ФВ:

, где Х_В – при возрастании, Х_y – при убывании.

Вариация объясняется тем, что отсчетное устройство не успевает за изменением величины.

·  Время установления показаний – промежуток времени от момента изменения измеряемой ФВ до момента успокоения указателя в точке равновесия. Это время определяет инерционность СИ.

·  Быстродействие СИ – определяется числом измерений в единицу времени.

МХ, определяющие качество измерений.

·  Сходимость результатов измерений – близость результатов измерений одной и той же ФВ, выполненных повторно теми же СИ, тем же методом, в тех же условиях, тем же наблюдателем.

·  Воспроизводимость результатов измерений – повторяемость результатов измерений одной и той же ФВ, полученной в разных местах, разными методами, разными операторами в разное время, но при одинаковых условиях.

·  Точность измерений – степень приближение результата измерения к истинному значению ФВ. Точность измерений определяется их погрешностью.

- Погрешность – разность между показаниями СИ и действительным значением ФВ.

За действительное значение ФВ принимается показание СИ более высокого ранга:

*для РСИ это ОСИ;

*для ОСИ – эталон 4-го разряда;

*для эталона 4-го разряда – эталон 3-го разряда и т.д.

Точность определяется показателями погрешности:

            абсолютной

            относительной

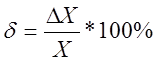
            приведенной 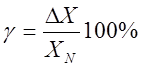      , где Х_N – нормированное значение.

            -  Основная погрешность – наблюдаемая при нормальных условиях;

            - Дополнительная погрешность – возникающая под действием величин влияния (температура, давление и т.д.);

По проявлению:

            - Систематическая погрешность – постоянна или закономерно изменяется основные составляющие: методологическая, инструментальная;

            - Случайная погрешность – порождает рассеяние результатов;

По режиму измерений:

            - Статическая погрешность – при измерении постоянных величин после завершения переходных процессов;

            - Динамическая погрешность – разность между погрешностью в динамическом режиме и статической погрешностью.

По взаимодействию с сигналом:

            - аддитивная погрешность (погрешность нуля) – неизменна во всем диапазоне сигнала.

            - мультипликативная погрешность – изменяющаяся пропорционально сигналу.

Класс точности СИ – обобщенная характеристика, выражается пределами допускаемых основной и дополнительной погрешностей, а также часто- вариацией показаний. Класс точности устанавливается в НД на СИ. У мерительных приборов – это абсолютная, а у аналоговых стрелочных – относительная (чаще – приведенная) погрешность.

Стрелочные электроприборы: пределы основной и дополнительной погрешности в заданных условиях (обычно – нормальных), пределы вариации, невозвращение стрелки к нулю.

Концевые меры: пределы отклонений от номинальной длины и плоскопаралельности, пределы изменения длины в течение года.

Присваиваются классы точности при разработке СИ приемочной комиссией. При поверках допускается понижать класс точности.

3. Погрешности измерений и обработка измерений.

Основной постулат измерений: измеренное значение ФВ всегда есть величина случайная, приближающаеся к истинному значению с определенной вероятностью Р(Х).

Это позволяет применять к изучению ошибок измерения методы теории вероятностей. В вероятностной модели результаты измерений X и ошибки измерений Z = X – a рассматриваются как случайные величины (а – истинное значение, к которому стремится Х), которые могут принимать любые действительные значения.

            Вероятность попадания значения величины Z в заданный интервал (Z₁, Z₂) определяется площадью под кривой зависимости плотности распределения вероятности р(z):

(1) p(Z) нормирована условием:                     (1а) рис.1.

            На практике в качестве меры вероятности выступает относительная частота m попадания в интервал (Z₁,Z₂) измеряемой величины Z  при общем числе испытаний n :

При устремление интервала (Z₁,Z₂) к нулю отношения стремится к вероятности.

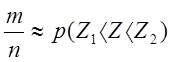
            Правило, по которому каждому значению Z определено значение плотности p(Z), а любому интервалу (Z₁,Z₂) – значение вероятности Р(Z₁<Z<Z₂), называется законом распределения вероятностей случайной величины Z.

Нормальный закон распределения

(закон Гаусса)

            В случае, когда погрешность образуется под действием большой совокупности независимых, также случайных, факторов, среди которых нет доминирующих, центральная предельная теорема гласит, что при этом погрешность будет распределена по нормальному закону.

            Принято считать, что нормальному закону распределения подчиняются погрешности измерения массы, величин твердости, других физических величин, линейных и угловых размеров.

            Плотность вероятности  нормального распределения описывается условно-непрерывной функцией

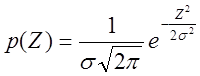                                                                                                                         (2)

            где:  - среднеквадратичное отклонение случайной величины Z от ее центра,

                    - дисперсия величины Z

                     D(Z) и характеризуют рассеяние величины Z и точность измерений.

Рисунок показывает, что при уменьшении  кривая нормального распределения сжимается вдоль оси p(z) следовательно: чем меньше , тем меньше разброс Z: тем быстрее убывает плотность распределения p(Z) с ростом Z. Рис.2