Качество: Основные понятия. Стандартизация, метрология, сертификация – основные инструменты обеспечения качества, страница 10

Сжатая кривая распределения ошибок говорит о высокой точности измерений.

            Кривая нормального распределения симметрична: p(-Z)=p(Z),

            Вероятность попадания случайной ошибки в симметричный интервал (-Z₁,Z₁) при нормальном распределении, исходя из общей формулы (1), рисунков1,2 вычисляется через интеграл вероятностей Ф(t), где :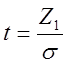

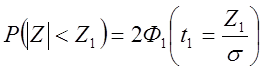       (3)

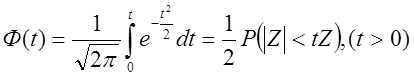    (3а)

            Интеграл вероятностей для диапазона (0,5) содержится в таблицах.

            Вероятность попадания случайной ошибки в любой интервал  (Z₁,Z₂), согласно (1), (3) и рис.1, в случае нормального распределения

                                         P(Z₁<Z<Z₂) = Ф(t₂) - Ф(t₁)                                                     (4)                                                         

Вероятность выхода случайной ошибки за границы равна:

                                                                                               (4а)

и также является табличной функцией. При t>2,5 её значения меньше 0,0125.

            На практике принимается, что случайные ошибки измерения ограничены по величине значением (правило трех сигм).

            Показатели точности измерения:

 

* Средняя квадратичные ошибки

* Дисперсия ошибки

* Вероятная ошибка  при                                                       (5)

* Средняя абсолютная ошибка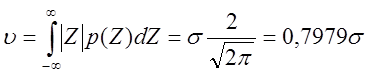

* Мера точности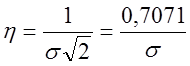

Общий нормальный закон распределения

            Если случайные ошибки Z подчиняются нормальному закону распределения с плотностью (2), то распределение результатов измерения x = a + z имеет плотность

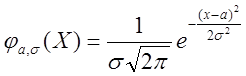           (6)

которая отличается от плотности (2) только сдвигом на величину а от оси отсчета, но имеет те же показатели точности.

Здесь а, как указано в начале – истинное значение измеряемой величины, к которому стремится X, и естественно, что распределение сгруппировалось вокруг него. Цент распределения сместился.   Рис.3.

            Такое распределение называется общим нормальным законом распределения с центром а.

            Для случайных ошибок центр равен нулю.

            В общем нормальном законе распределения могут быть определены теоретически средние – иначе моменты распределения. Исходя из основного постулата измерений, считаем, что ищется случайная величина; обозначим её Х. Точнее, имеется математическое ожидание М(Х) – по другому начальный момент 1-го порядка:

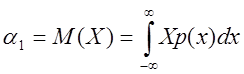, р(х) – плотность распределения Х.    (7)

По определению - центр распределения величины Х. Если распределение Гауссово, то .

Отклонение случайной величины Х от ее центра называется центрированной случайной величиной (ЦСВ)

По смыслу она и есть текущая ошибка Z.

            Моменты распределения случайной величины Х, взятые от её ЦСВ, называются центральными моментами .

            Центральный момент первого порядка при нормальном распределении всегда равен нулю

            Центральный момент второго порядка – называется дисперсией величины Х

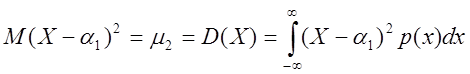                                                  (8)

            При общем нормальном распределении дисперсия равна квадрату среднеквадратичного отклонения, случайной величины Х  от ее центра

            характеризуют рассеяние случайной величины Х.

            Если известна функция р(х) и она непрерывна, то теоретическое среднее, определенное по формуле (7) – математическое ожидание М(Х) случайной величины Х принимается за искомое истинное значение с параметрами рассеяния .

            При этом показатели точности измерения находятся по соотношениям (5).

3.1.Оценка истинного значения измеряемой величины при общем нормальном распределении.

            Рассмотренные выше соотношения (1-8) и способы определения показателей точности измерений по выражениям (5) являются теоретическими и могут использоваться для практики только в том случае, если:

- точно известно, что кривая распределения – нормальная,

- пределы изменения t столь значительны, что значения функции 1-2Ф(t) на границах пренебрежимо малы,

- величины определены достоверно, как теоретические значения.

Тогда М(Х), определенное по (7) есть истинное а.

            Но фактически кривые распределения р(х) считаются непрерывными условно, т.к. любой процесс отсчета случайной величины  есть процесс дискретный (в том числе процесс измерений). Т.е. величина Х – это счетное множество , состоящее из конечного числа n независимых величин (независимых измерений).

            Поэтому при обработке результатов измерений производится не определение, а оценка истинного значения измеряемой величины.

            Ясно, что при этом непрерывные функции заменяются множеством Х независимых величин (числом n), а операции интегрирования – операциями суммирования по данному множеству.

Точечная оценка значения а.

            Произвести точечную оценку истинного значения измеряемой величины а, это значит:

            1).указать такую функцию от результатов измерений, которая дает достаточное приближение к значению а.

            2).указать границы интервала , который с заданной вероятностью Р покрывает истинное значение а.

            Т.е. находится область значений , внутри которой с вероятностью Р (надежностью Р) находится истинное значение а.

            Такая оценка ещё называется доверительной оценкой, вероятность Р – доверительной вероятностью или надежностью оценки, а интервал - доверительным интервалом, а его границы – доверительными границами.

            Точечная (доверительная) оценка должна обладать свойствами:

·  Несмещенности – когда теоретическое среднее (М(Х)) совпадает с истинными значением а,

·  Состоятельности – когда при устремлении числа измерений n к бесконечности Х по вероятности стремится к а. То есть при  для любого малого  вероятность  стремится к единице.

·  Эффективности – когда несмещенная оценка имеет наименьшее рассеяние среди всех несмещенных оценок Х по результатам измерений.

При общем нормальном законе распределения вероятностей случайной величины оценка истинного значения искомой величины несмещенная, состоятельна и эффективна.