Качество: Основные понятия. Стандартизация, метрология, сертификация – основные инструменты обеспечения качества, страница 11

Из изложенного следует, что в качестве точечной оценки истинного значения величина а должно приниматься среднеарифметическое значение результатов измерений (СА):

·  Для равноточных измерений:

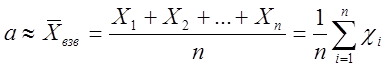,                                                         (9)

где: - обозначение среднеарифметического,

         n – число измерений

        - отдельная (i-я) измеренная величина.

·  Для неравноточных измерений – взвешенное среднее арифметическое

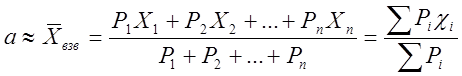  ,                                                       (9а)

где: Р_i – веса измерений при условии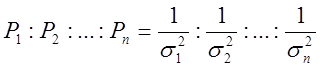

Особенности СКО:

Среднеквадратичная ошибка среднеарифметического при конечном числе n всегда меньше СКО измерений отдельных величин Х:

            Доверительный интервал при известной :

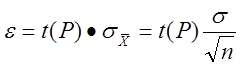                                                                                                        (10)

где: n – число измерений

t = t(P) – определяется по заданной доверительной вероятности Р их таблиц для Р=2Ф(t) (формулы 3,4).

            Данная оценка, т.е. через нахождение t(P) по табличным значениям интеграла вероятностей Р=2Ф(t), возможна только при известной точности измерений: известны D(X),  .

3.2. Доверительная оценка при неизвестной точности измерений

            На практике, когда количество измерений n ограниченно, точность измерений заранее не известны. Тогда в качестве оценки также служит среднеарифметическое значение результатов измерений, (- математическое ожидание никто не отменял) определяемое по формуле (9, 9а), но взамен СКО  используется эмпирический стандарт СКО

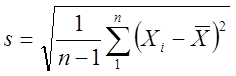                                                                                                      (11)

что совершенно очевидно следует из преобразования (8) в дискретную форму.

Здесь  - число степеней свободы

            А доверительный интервал

теперь зависит нет только от доверительной вероятности Р, но и от числа степеней свободы (числа измерений):

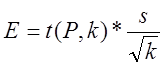                                                                                                             (12)

множитель  - определяется по табличным значениям распределения  Стьюдента (распределения вероятностей   для )

Чем больше испытаний n, тем ближе t(P,k)  к   t(P) по интегралу вероятностей  Р=2Ф(t).

            При данной оценке доверительный интервал значительно шире, чем при известных    и   .

            Оценка по правилу трех сигм:

Отклонение истинного значения от СА результатов измерений не превосходит устроенной СКО этого среднего значения

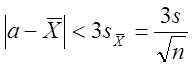                                                                                                                 (13)

Надежность оценки

Таб.1.

Необходимое количество измерений

Необходимое количество измерений определяется в зависимости от надежности Р и отношения 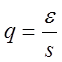, где s – будущий эмпирический стандарт:

Таб.2

Р q	0,90	0,95	0,99
1,0	5	7	11
0,5	13	18	31
0,1	273	387	668
0,05	1084	1540	2659

Исключение грубых ошибок

·  Наиболее простой способ состоит в применении правила трех сигм: все значения, выходящие за пределы интервала , считают грубыми ошибками.

·  Более строгий способ:

- для «выскакивающего» значения  определяем отношение .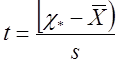

- сравниваем t с табличными критическими значениями   для заданной надежности Р и числа испытаний n

- если , то  - грубая ошибка

  при Р=0,95

Табл.3

n	5	7	10	15	20	50	100
	3,04	2,62	2,37	2,22	2,145	2,03	1,994

3.3. Проверка нормальности распределения

            Все приведенные доверительные оценки основаны на гипотезе нормальности закона распределения случайных ошибок измерения.

            Если возникло сомнение в нормальности закона распределения , то надо произвести достаточно большое число измерений и произвести проверку по одному из критериев.

·  Предварительная оценка

Предварительная, весьма грубая оценка производится через коэффициент вариации

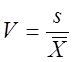                                                                                                          (14)

Если , можно принимать нормальность распределения полученных результатов.

·  Приближенный метод поверки

В этом случае определяются центральные моменты третьего  и четвертого  порядка. Их оценка:

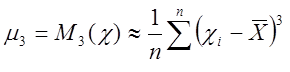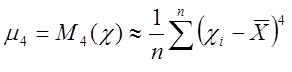;                                 (15)

В случае нормального распределения ,                                    (16)

При этом более точно сравнить следующие величины:

показатель асимметрии 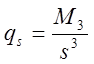  и   эксцесс  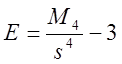                                     (17)

с их среднеквадратическими ошибками

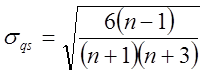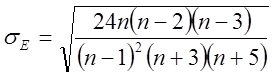,                                                      (18)

Если хотя бы одна из характеристик по абсолютной величине значительно (в 2-3 раза) превосходит свою СКО, то нормальность распределения – под сомнением и требует проверки более тщательным методом.

·  Проверка по критерию соответствия  (хи – квадрат) .

- Результаты измерений (свободные от систематических ошибок) группируются по интервалам, покрывая всю ось . Количество данных в каждом интервале – не менее пяти. В каждом интервале  подсчитывают число   результатов.

- Вычисляют вероятность   попадания в эти интервалы для случая нормального распределения:

,

где Ф – интеграл вероятностей по ф.(3,4) – табличный,

;                               

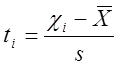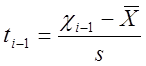
- Вычисляем сумму 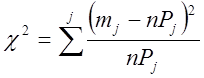                 (19)

где: j – число всех интервалов ,   - число всех результатов.

            Если полученное по (19) значение   будет больше соответствующего критического, то с надежностью Р распределение отличается от нормального.

            Малая величина  не служит доказательством нормальности распределения.