![]() Министерство
образования Республики Беларусь
Министерство
образования Республики Беларусь
Белорусский Национальный Технический Университет
Кафедра“Гидропневмоавтоматика и гидропневмопривод”
Группа 101714
Курсовая работа
по дисциплине “Механика жидкости и газа”
Выполнил:
Руководитель:
Минск 2007
Содержание
Введение 4
Задача №1. Движение газового потока в сопле Лаваля 5-14
Задача №2. Потенциальное течение несжимаемой жидкости 15-21
Задача №3.Применение метода Кармана-Польгаузена к расчету
ламинарного пограничного слоя 22-28
Задача №4. Определение зависимости потребного диаметра
трубопровода от величины абсолютной шероховатости 29-31
Заключение
2
Расчетно-графическая работа №1
Движение газового потока в сопле Лаваля
Задано:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Расчетное тело - водород H2,
.
Расчетное тело - водород H2, ![]() ,
, ![]()
1. Скорость звука в начальном сечении
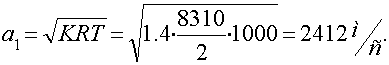
Число Маха на входе
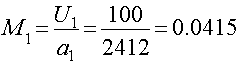 .
.
Из табл. 1.1 находим
![]()
Параметры торможения:
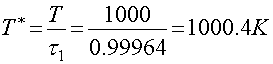 ;
;
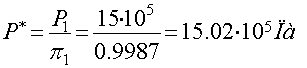 ;
;
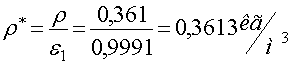 ;
; 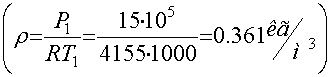
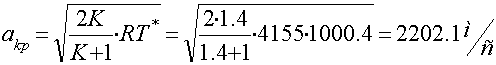 .
.
2. Площадь входного сечения
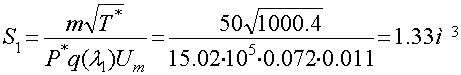
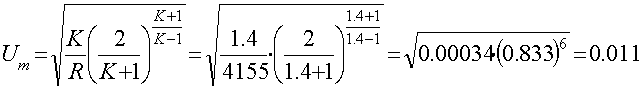 Диаметр входного сечения
Диаметр входного сечения
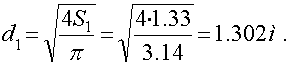
Площадь критического сечения
![]()
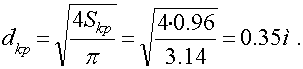
Газодинамические функции в выходной части сопла
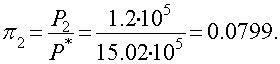
Остальные значения находим по табл. 1.1 при известном значении ![]()
![]()
Площадь и диаметр выходного сечения сопла
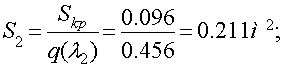
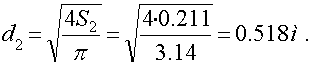
3. Длина дозвуковой (сужающейся) части сопла
![]()
Длина сверхзвуковой части сопла
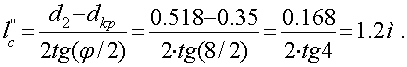
Полная длина сопла
![]()
4.
Сначала делим сужающуюся
часть сопла по длине на пять примерно равных интервалов (0,14, 0,28, 0,42, 0,56,
0,7 м). Два последних интервала делим еще пополам (0,49 и 0,63
м). По формуле 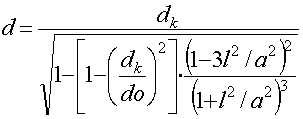
рассчитываем диаметр сопла в каждом из сечений и
соответственно площадь поперечного сечения. Пользуясь формулой ![]() , находим
, находим ![]() и тем самым все газодинамические
функции в последующем сечении. По значениям этих функций и параметрам
торможения определяем основные параметры. Результаты расчетов сводим в таблицу
1.
и тем самым все газодинамические
функции в последующем сечении. По значениям этих функций и параметрам
торможения определяем основные параметры. Результаты расчетов сводим в таблицу
1.
5.
Сверхзвуковую часть сопла
разбиваем на интервалы по давлению (в нашем случае удобно разбить на интервалы
по 0.1 МПа). По давлению в каждом сечении определяем 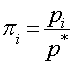 , а по нему все остальные
газодинамические функции и параметры. Располагая для удобства начало координат
в критическом сечении, вычисляем
, а по нему все остальные
газодинамические функции и параметры. Располагая для удобства начало координат
в критическом сечении, вычисляем ![]() .
Результаты расчетов заносим в таблицу 2.
.
Результаты расчетов заносим в таблицу 2.
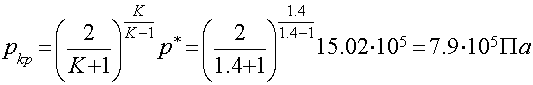
6.
Предположим, что скачок
уплотнения находится в критическом сечении. Профиль сопла сохраним таким же,
как и в расчетом режиме истечения. Сечения выбираем (только для удобства)
такими же, как и при сверхзвуковом истечении с известным ![]() в них. По формуле
в них. По формуле ![]() можно найти
можно найти ![]() (истечение за скачком
дозвуковое), а следовательно и все газодинамические функции. Так как параметры
торможения при током истечении сохраняют постоянное значение, можно рассчитать
изменение основных параметров по длине сопла (таблица 3).
(истечение за скачком
дозвуковое), а следовательно и все газодинамические функции. Так как параметры
торможения при током истечении сохраняют постоянное значение, можно рассчитать
изменение основных параметров по длине сопла (таблица 3).
7.
Предположим, что скачок
уплотнения находится в каком-либо сечении за критическим. В сечении, где
имеется скачок определяем ![]() по
формуле
по
формуле ![]() , а по формуле
, а по формуле 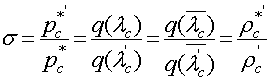 - параметры торможения за
скачком. Остальные расчеты не отличаются от ранее изложенных для дозвукового
течения. Результаты расчетов заносятся в таблицу 4. Для простоты сечения удобно
выбирать такими же, как и при расчете сверхзвукового истечения из сопла.
Близкие к критическому сечения выбирать не рекомендуется из-за малого отличия
от параметров для нерасчетного режима. Поэтому расчеты течения со скачком
проводились, начиная с третьего сечения.
- параметры торможения за
скачком. Остальные расчеты не отличаются от ранее изложенных для дозвукового
течения. Результаты расчетов заносятся в таблицу 4. Для простоты сечения удобно
выбирать такими же, как и при расчете сверхзвукового истечения из сопла.
Близкие к критическому сечения выбирать не рекомендуется из-за малого отличия
от параметров для нерасчетного режима. Поэтому расчеты течения со скачком
проводились, начиная с третьего сечения.
8. На рис. 1 представлен профиль сопла, а на рис. 2 – изменение площади поперечного сечения по длине. На рис. 3-7 показано изменение основных величин по длине сопла для расчетного 1 и нерасчетного 2 режимов течения со скачком в сечениях 3-7.
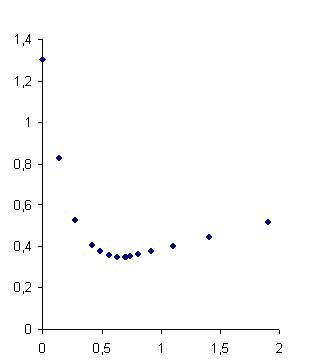 рис.
1
рис.
1
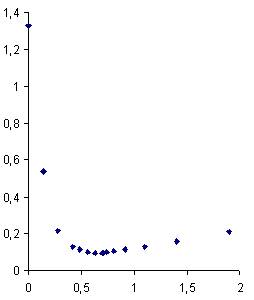 рис. 2
рис. 2
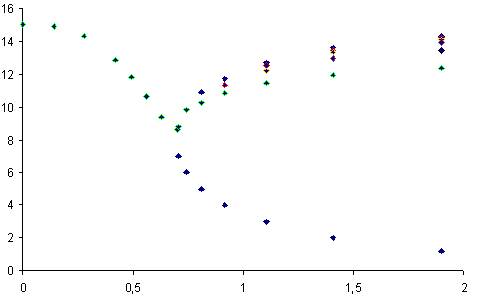 рис. 3
рис. 3
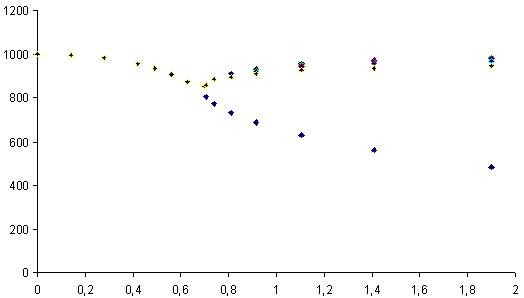 рис
4
рис
4
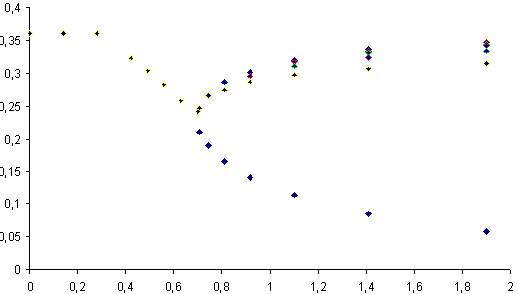 рис. 5
рис. 5
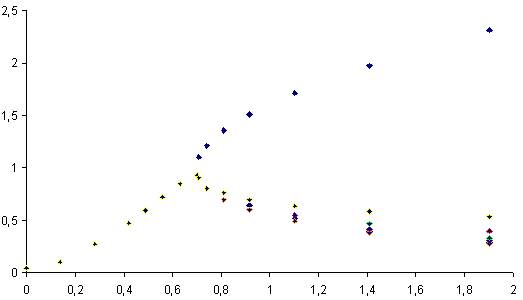 рис. 6
рис. 6
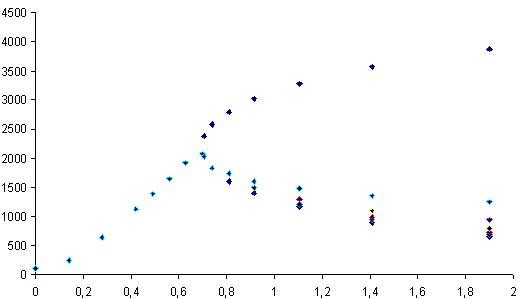 рис. 7
рис. 7
2
Расчетно-графическая работа №2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.