Движение газового потока в сопле Лаваля. Потенциальное течение несжимаемой жидкости. Применение метода Кармана-Польгаузена к расчету ламинарного пограничного слоя, страница 2

Потенциальное течение несжимаемой жидкости

Задано:        

 Обтекание круглого бесконечного цилиндра с r₀=0.25 м потоком U₀=10 м/с с циркуляцией Г=2 м²/с.

1.  Построить графики линий тока и линий равного потенциала течения       

Разложим sin в ряд Тейлора:

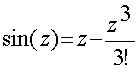
Тогда с учетом   комплексный потенциал течения примет вид

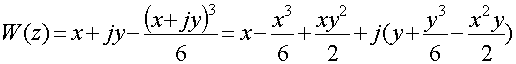
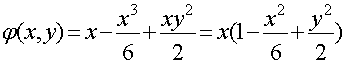
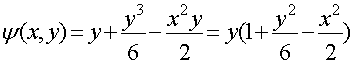
Уравнение линий равного потенциала в декартовой системе координат

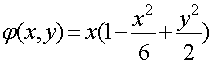
Уравнение линий тока в декартовой системе координат

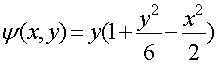
По полученным данным строим линии равного потенциала и линии тока

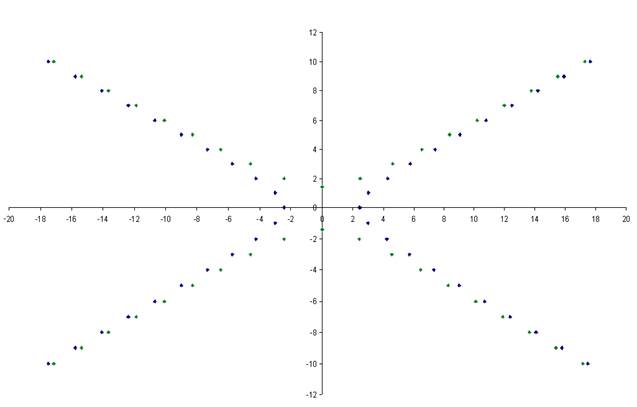
Рисунок 1.– Линии равного потенциала и линии тока

Определим скорости ;  .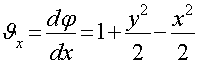

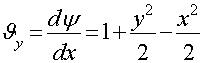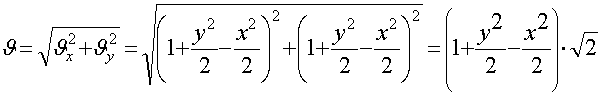
Находим давление в любой точке потока несжимаемой жидкости из уравнения Эйлера:

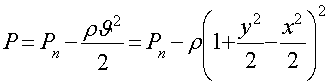
Согласно условию физической реальности необходимо, чтобы ни в одной точке потока не было P<0, т.е. во всех точка потока отсутствовала кавитация:

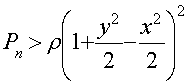
2.  По заданному комплексному потенциалу скоростей обтекания цилиндра с циркуляцией требуется:

1)  Определить тип обтекания.

2)  Вычислить и построить в масштабе:

а) функцию тока для трех характерных значений произвольных постоянных;

б) распределение окружной составляющей скорости; в) график зависимости коэффициента давления от угла .

3)  Рассчитать коэффициент подъемной силы.

Комплексный потенциал имеет вид:

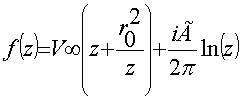
1) Определим критические углы (углы в которых Р=0):

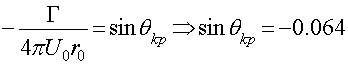
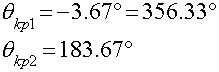
2) a) Выделяя мнимую часть в выражении, получим функцию тока 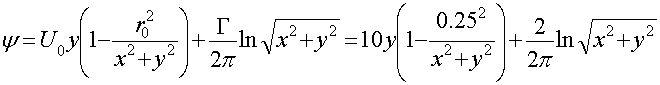Определим  в характерных трех точках:

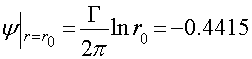
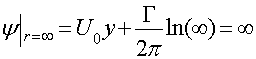
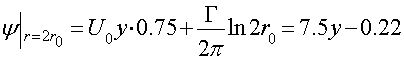
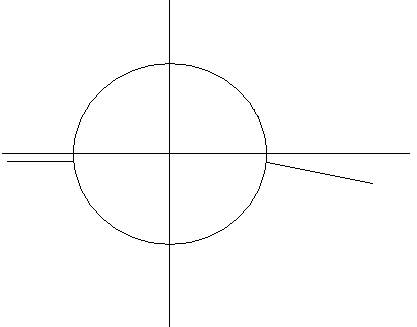
Рисунок 2.– Линии тока при обтекании цилиндра с циркуляцией б) Определим распределение окружной составляющей скорости  на поверхности цилиндра

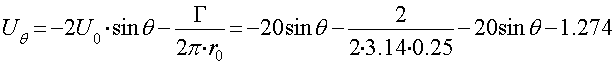
На основании этой формулы заполним таблицу

	0	30	60	90
	-1,274	-11,274	-18,5945	-21,274

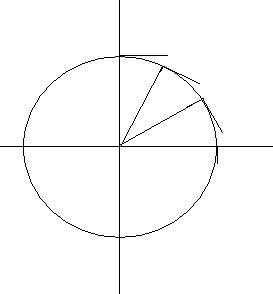
Рисунок 3. – Распределение окружной составляющей скорости на поверхности цилиндра в) Определим зависимость коэффициента давления от угла

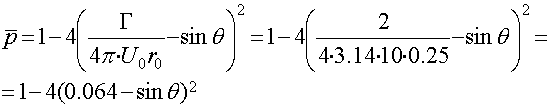
	90	60	30	0	-30	-60	-90
	-2,504	-1,573	0,240	0,984	-0,272	-2,460	-3,528

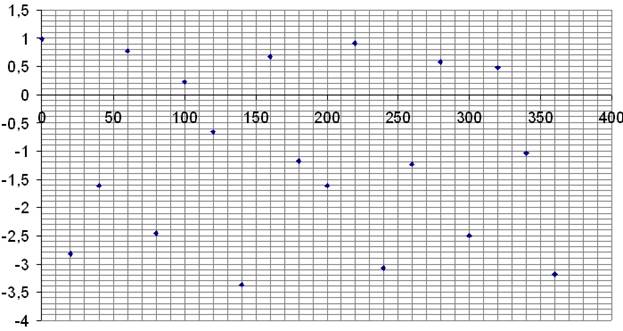
Рисунок 4. - Построим график зависимости

Рисунок 5. – Полярная диаграмма распределения на поверхности цилиндра.

3) Определим коэффициент подъемной силы:

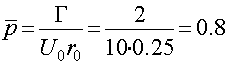
4

Расчетно-графическая работа №3

Применение метода Кармана-Польгаузена к расчету

ламинарного пограничного слоя

Задано:

      Вычислить по методу Кармана-Польгаузена основные характеристики ламинарного пограничного слоя, сравнить с точным решением при  и следующими граничными условиями для выбора профиля:

При ,  ;

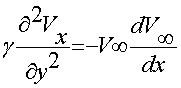на границе пограничного слоя при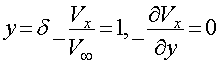

Построить график зависимости , точный и расчетный профили скоростей  при заданном значении  и для однородного потока () .

Идея метода Кармана-Польгаузена состоит в замене неустойчивого точного распределения скоростей в пограничном слое специально подобранным распределением, удовлетворяющим граничным условиям задачи.

Из заданных граничных условий следует, что полином должен быть третьего порядка

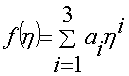
с граничными условиями для функции :

при    ;

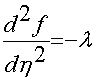при     f=1, .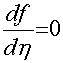

Следовательно, для определения коэффициентов  получим систему алгебраических уравнений

;

;

.

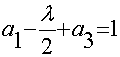Приведенная система легко вычисляется с помощью теории определителей, а для коэффициентов  следующие выражения:

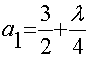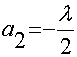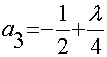,  ,  ,  тогда

,   .

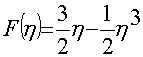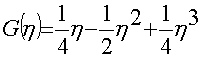Для построения характеристики  определим значения коэффициентов , входящих в ее выражение:

;

;

;

;

 .

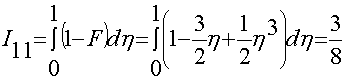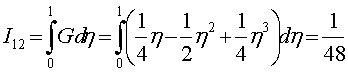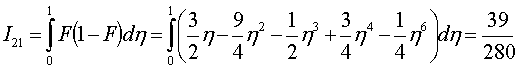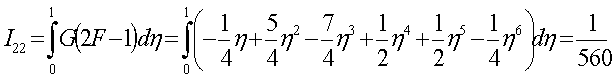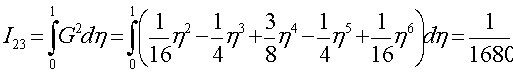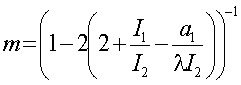, где  и ; тогда

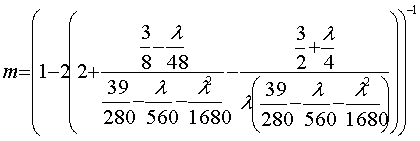                        (1)

Т.к. 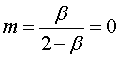,  расчеты необходимо выполнять в области положительных значений . Составим таблицу 3.1, таблица 3.1

	0	1	2	3	4	5	6	7	8	9	10
	0	0.0575	0.1429	0.2628	0.4104	0.5449	0.6000	0.5503	0.4398	0.3214	0.2203

Построим график  по ее значениям (рисунок 1)