Движение газового потока в сопле Лаваля. Потенциальное течение несжимаемой жидкости. Применение метода Кармана-Польгаузена к расчету ламинарного пограничного слоя, страница 3

 

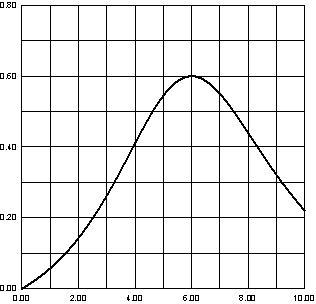
Рисунок 1– График зависимости

Таким образом, вычисления необходимо выполнить при m=0. На графике для соответствующего m определим ().

Точное вычисление получаем.

Теперь можно вычислить основные параметры потока:

.

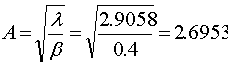По формуле для напряжения трения определяем величину

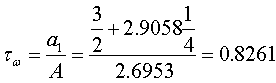, сравниваем ее с точным значением: .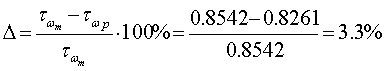

Полученное значениесоответствует степени точности самого метода.

Вычисляем условные толщины ламинарного пограничного слоя:

;

.

Сравниваем полученные значения с точными:

,   .

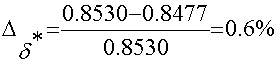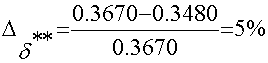Для нахождения значений распределения скоростей используем формулу

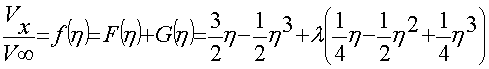
по значениям таблицы 3.2 (рисунок 2)

таблица 3.2

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
	0	0.2695	0.5390	0.8085	1.0781	1.3476	1.6171	1.8866	2.1562	2.4257	2.6952
	0	0.2083	0.3889	0.5432	0.6726	0.7783	0.8617	0.9242	0.9672	0.9920	1.0000

 

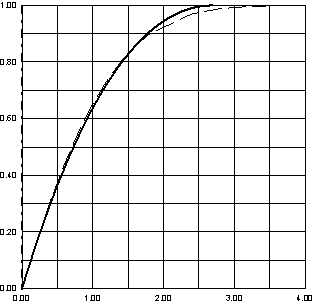
Рисунок  2 – Профили скоростей при

Вычислим распределение основных параметров для данного профиля в случае однородного внешнего потока :

;

;

;

;

;

,   .

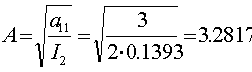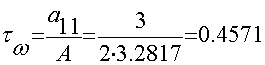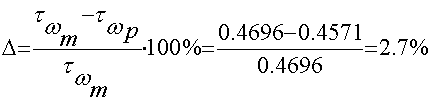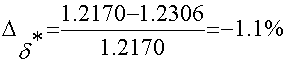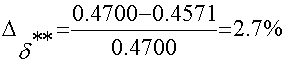В таблице 3.3 представлены расчеты профиля скоростей для однородного потока.

таблица 3.2

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
	0	0.3281	0.6563	0.9845	1.3126	1.6408	1.9689	2.2971	2.6253	2.9534	3.2816
	0	0.1495	0.2960	0.4365	0.5680	0.6875	0.7920	0.8785	0.9440	0.9855	1.0000

Точный и расчетный профили представлены на рисунке 3.

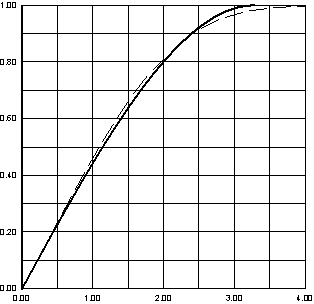
Рисунок  3 – Профили скоростей при

Проведенное исследование заданного профиля скоростей свидетельствует о возможности получения хороших результатов с помощью метода Кармана-Польгаузена по основным интегральным характеристикам в области положительных значений параметра давления.

Введение

Гидромеханика – наука, изучающая движение и равновесие жидкостей, а также взаимодействие между жидкостями и твердыми телами, полностью или частично погруженными в жидкость.

Для решения различных проблем связанных с различными свойствами различных сред, поэтому механика делится на ряд самостоятельных дисциплин:

·  гидромеханика, изучающая жидкости и их взаимодействие с различными средами;

·  газовую динамику, изучающую свойства газов;

·  теорию упругости и др.

В гидромеханике широко используются математические методы, поэтому результаты обладают правильностью и точностью. Кроме того, эксперименты, проводимые при первичном изучении явлений, служат для составления расчетных моделей. Из этого можно сделать вывод, что в гидродинамике нельзя обойтись без экспериментов.

В данное время изучение данных наук необходимо, т.к. во все больших отраслях промышленности используются гидравлические и пневматические системы. Данные системы позволяют упростить устройство и дают возможность сделать устройства позволяющие расположить его в недоступном или сложно доступном месте, не вызывая при этом больших сложностей.

Список используемых источников

1.  Методические указания к выполнению расчетно-графических работ,

В.П. Автушко, И.А. Веренич, Мн., 1996

2. Справочное пособие по гидравлике, гидромашинам и гидроприводам, под ред. Б.Б. Некрасова, Мн., 1985

3. Задачник по гидравлике, гидромашинам и гидроприводу, учеб. пособие, Б.Б. Некрасов, И.В. Фатеев, Ю.А. Белеков и др., М., 1989