Задача 1. Определить давления рА и рБ в резервуарах А и Б, если разность уровней ртути, залитой в дифференциальный манометр, равна h. Пружинный манометр, подключённый к резервуару Б, показывает ро. В резервуарах находится вода. Плотность ртути rр = = 13600 кг/м3.
Исходные данные: h = 300 мм; ро = 0,03 МПа.
Рис.1. Расчётная схема дифференциального манометра
Решение. Избыточное давление воды в баке Б равно показанию пружинного манометра:
рБ = ро = 0,03 МПа = 30000 Па.
Давление в дифференциальном манометре на уровне 2 – 2 определится по формуле:
р2 = ро – rg(h1 + h).
Давление в дифференциальном манометре на уровне 1 – 1 определится по формуле:
р1 = р2 + rрgh.
Давление в баке А на уровне 0 – 0 определится по формуле:
рА = р1 + rgh1.
Подставляем предыдущие выражения в последнюю формулу и рассчитываем значение давления в баке А:
рА = р1 + rgh1 = р2 + rрgh + rgh1 = ро – rg(h1 + h) + rрgh +
+ rgh1 = ро – rgh1 – rgh + rрgh + rgh1 = ро – rgh + rрgh =
= ро + (rр – r)gh = 30000 + (13600 – 1000)×9,81×0,3 = 67082 Па.
Задача 2. Определить, чему равен вакуум рвак во всасывающем трубопроводе насоса, если внутренний диаметр труб d = 75 мм, расход воды Q = 5 л/с, эквивалентная шероховатость труб D = = 1,0 мм. Принять коэффициент сопротивления приёмной сетки, включая обратный клапан x = 4,2, а коэффициент сопротивления колена xк = 0,68 (угол b = 60°). Построить напорную и пьезометрическую линии.
Исходные данные: zв = 3,5 м; l1 = 4,5 м; l2 = 4,2 м.
Рис.3. Схема насосной установки
Решение. Для сечений 1-1 и 2-2 записываем уравнение Бернулли /1, с.50/:
z1 + ![]() .
.
Учитывая, что z2 – z1 = zв; р1 = 0; р2 = –рвак, v1 = 0; v2 = v, упрощаем исходное уравнение:
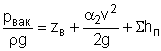 . (1)
. (1)
Скорость воды в трубопроводе:
v = ![]() м/с.
м/с.
Число Рейнольдса:
Re = ![]() .
.
Определяем отношение:
500![]() < Re = 84750 – режим
движения жидкости турбулентный, зона квадратичного сопротивления /1, с.72/. Коэффициент
гидравлического трения для этой зоны равен:
< Re = 84750 – режим
движения жидкости турбулентный, зона квадратичного сопротивления /1, с.72/. Коэффициент
гидравлического трения для этой зоны равен:
l = 0,11×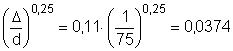 .
.
Потери напора по длине трубопровода /1, с.65/:
hдл = ![]() м.
м.
Потери напора в местных сопротивлениях /1, с.83/:
hм = ![]() м.
м.
Суммарные потери напора:
Shп = hдл + hм = 0,282 + 0,318 = 0,60 м.
Подставляем полученные значения в уравнение (1) и определяем величину вакуума:
![]() ;
;
рвак = 1000×9,81×(3,5 + 0,068 + 0,6) = 40888 Па.
Для построения пьезометрической и напорной линии рассчитываем составляющие напора в характерных сечениях:
![]() м;
м;
![]() м;
м;
hдл1 = ![]() м;
м;
hдл2 = ![]() м;
м;
hвх = ![]() м;
м;
hпов = ![]() м.
м.
Рис.4. Построение напорной и пьезометрических линий
Задача 3. Определить расход воздуха, вытекающего через сопло dс, если зазор между торцом сопла и заслонкой равен х. Сжимаемостью воздуха пренебречь. Принять коэффициент расхода для диафрагмы dо и сопла равными 0,72.
Исходные данные: dо = 1,4 мм; dс = 2,8 мм; ро = 7,5 кПа;
х = 550 мкм.
Рис.5. Расчётная схема сопла
Решение. По теореме о количестве движения для струи давление в сопле определяется по формуле:
![]() , где r = 1,2 кг/м3 – плотность воздуха.
, где r = 1,2 кг/м3 – плотность воздуха.
Откуда расход через кольцевую поверхность зазора будет равен:
![]() . (1)
. (1)
Расход через само сопло определяется по формуле:
![]() . (2)
. (2)
Расход воздуха через диафрагму:
![]() . (3)
. (3)
Так как решение системы из трёх уравнений с тремя неизвестными в общей форме достаточно затруднительно, то подставляем известные числовые значения и решаем систему относительно расхода Q.
Из первого уравнения выражаем рс через Q:
![]() ;
;
![]() ;
;
рс = 0,05123×1012Q2.
Из второго уравнения выражаем давление р через расход Q:
![]() ;
;
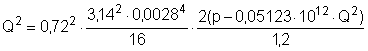 ;
;
Q2 = 32,725×10-12×(р – 0,05123×1012×Q2);
Q2 + 1,6765Q2 = 32,725×10-12×р;
р = 0,08179×1012Q2.
Подставляем значение для р в уравнение (3) и решаем его относительно расхода Q:
![]() ;
;
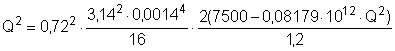 ;
;
Q2 = 2,04534×10-12×(7500 – 0,08179×1012×Q2);
Q2 + 0,16729Q2 = 1,534×10–8;
Q2 = 9,170×10–8;
![]() м3/с = 0,303 л/с.
м3/с = 0,303 л/с.
Список литературы
1. Гидравлика, гидравлические машины и гидроприводы. Методические указания. Сост. В.И. Погорелов. – Л.: ЛТА, 1984. – 32 с.
2. Справочное пособие по гидравлике, гидромашинам и гидроприводам. Под ред. Б.Б. Некрасова. – Мн.: Выш. шк., 1985. – 382 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.