Решение дифференциальных уравнений 3-го порядка методом Адамса-Бэшфорта

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Системного Анализа и Управления

Работа №2

Курс: «Вычислительная математика»

Тема: «Решение дифференциальных уравнений 3го порядка»

Выполнила:  ст. гр. 2082/1 

Калабанова А. С.

Проверил:  Кирсяев А. Н.

Санкт-Петербург

2006

Постановка задачи

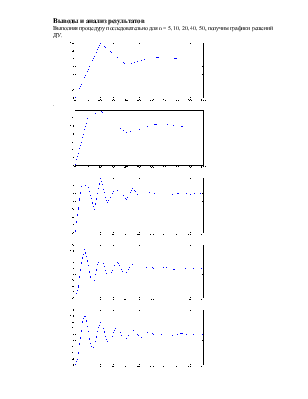
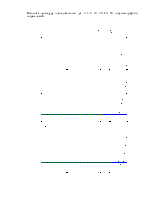
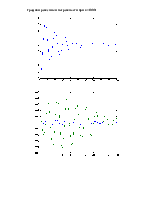
Исследовать зависимость устойчивости и погрешности решения дифференциального уравнения заданным численным методом. Сравнить полученное решение с аналитическим решением и результатом использования стандартного сольвера Matlab. Дифференциальное уравнение имеет вид: a₀ y’’’(t) + a₁ y’’(t) + a₂ y’(t) + y(t) = 10. Начальные условия: y(0) = y’(0) = y’’(0) = 0. Интервал: t Є [0, t_m].

Данные: a₀ = 4.9682; a₁ = 4.372; a₂ = 1.568; t_m = 100 [с]. Метод Адамса-Бэшфорта 2го порядка.

Методы решения и формулы

Любое дифференциальное уравнение n-го порядка может быть представлено, как система дифференциальных уравнений n-го порядка. Поэтому для решения заданного диф. уравнения оно сначала представляется в виде системы X’(t) = F(t,X(t)), где F(t,X(t)) = A*X(t) + Ф(t). Для нашего уравнения имеем следующую систему:

 ;  ;  ;  .

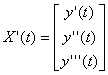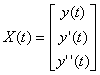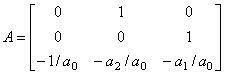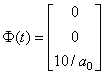Известно, что задача Коши для дифференциального уравнения не всегда имеет аналитическое решение. Поэтому для численного решения дифференциальных уравнений существуют различные методы приближённого решения. Все они основаны на вычислении значений решений уравнения в конечном числе точек, что называется методом разностных уравнений. Предполагается, что вычисления проводятся в равноудалённых точках, например, через равные промежутки времени. Величина промежутков времени называется шагом.