Решение дифференциальных уравнений 3-го порядка методом Адамса-Бэшфорта, страница 3

Блок-схема программы

AB2(n)

Входные данные: n – количество шагов интегрирования.

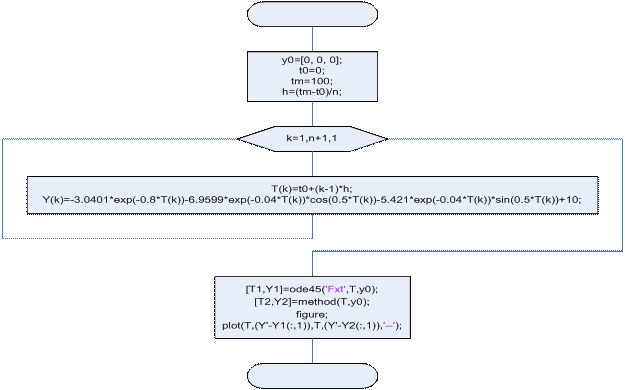
method(tspan, y0)

Входные данные: tspan – вектор разбиения отрезка интегрирования;

                               y0 – вектор начальных условий.

Выходные данные: T – вектор разбиения отрезка интегрирования;

                                 Y – вектор приближенных решений в точках разбиения.

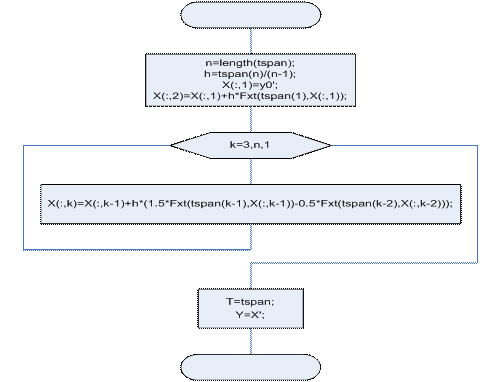
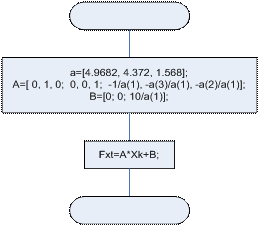
Fxt(t, Xk)

Входные данные: t – значение аргумента;

                               Xk – значение вектор функции X(t).

Выходные данные: Fxt – значение функции F(t, X(t)).

Текст программы

AB2.m

%Процедура исследования устойчивости

%и погрешности решения диф. уравнения

%методом Адамса-Бэшфорта 2го порядка

function AB2(n) %процедура от числа шагов n

y0=[0, 0, 0];   %вектор начальных условий

t0=0; tm=100; %концы интервала интегрирования

%разбиение интервала и значения аналитического решения

h=(tm-t0)/n;

for k=1:n+1

    T(k)=t0+(k-1)*h;

    Y(k)=-3.0401*exp(-0.8*T(k))-6.9599*exp(-0.04*T(k))*cos(0.5*T(k))-5.421*exp(-0.04*T(k))*sin(0.5*T(k))+10;

end

%построение графиков решения

[T1,Y1]=ode45('Fxt',T,y0);

[T2,Y2]=method(T,y0);

figure;

plot(T,(Y'-Y1(:,1)),T,(Y'-Y2(:,1)),'--');

method.m

%Метод Адамса-Бэшфорта 2го порядка

function [T,Y]=method(tspan, y0)

n=length(tspan);    %кол-во шагов и точек разбиения

h=tspan(n)/(n-1);   %шаг

X(:,1)=y0';  %начальные значения

X(:,2)=X(:,1)+h*Fxt(tspan(1),X(:,1));  %первый шаг явным методом Эйлера

for k=3:n

    X(:,k)=X(:,k-1)+h*(1.5*Fxt(tspan(k-1),X(:,k-1))-0.5*Fxt(tspan(k-2),X(:,k-2)));

end

T=tspan;

Y=X';

Fxt.m

%Система диф.ур-ний, эквивалентная исходному

%X'(t)=F(X(t),t)=A*X(t)+B(t)

function Fxt=Fxt(t, Xk) %F(t,X(t))