Решение дифференциальных уравнений 3-го порядка методом Адамса-Бэшфорта, страница 2

Для метода Адамса-Бэшфорта 2го порядка мы имеем следующую разностную схему:

Чтобы начать вычисление с помощью этого метода, необходимо найти решение в точке x₁. Для этого используют какой-либо одношаговый метод того же порядка точности, например явный метод Эйлера. Таким образом, для первого шага имеем

Аналитическое решение заданного диф. уравнения:

Итак, дано дифференциальное уравнение:

Корни характеристического многочлена для данного уравнения следующие:

Соответствующие им частные решения диф. уравнения имеют вид:

Общее решение нашего диф. уравнения имеет вид:

где  есть полином той же степени, что и стоящий в правой части дифференциального уравнения, то есть представляет собой константу.

Имея начальные условия  y(0) = y’(0) = y’’(0) = 0 и получив из диф. уравнения четвертое условие y’’’(0) = 10 / a₀ , получим следующую систему  уравнений с четырьмя неизвестными:

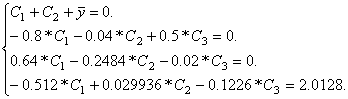
Решая эту систему, находим

Таким образом, заданное дифференциальное уравнение решено аналитически:

Структура данных и программы

Программа состоит из следующих модулей:

1. AB2.m – Процедура AB2(n), строящая для разного числа шагов n графики погрешностей решения сольвера ode45 пакета Matlab и решения, полученного численным методом Адамса-Бэшфорта 2го порядка.
2. method.m – Функция method(tspan, y0) метода Адамса-Бэшфорта 2го порядка. Принимает на вход интервал интегрирования tspan и вектор начальных значений y0 и выдает на выходе разбиение интервала интегрирования и приближенные решения уравнения в точках разбиения, полученные численным методом.
3. Fxt.m – Функция Fxt(t, Xk), представляющая заданное диф. уравнение в виде системы диф. уравнений. Принимает на вход значения t и X(t) и выдает на выходе вектор значений F(t, X(t)).