Решение дифференциальных уравнений 3-го порядка методом Адамса-Бэшфорта, страница 4

a=[4.9682, 4.372, 1.568]; %коэффициенты диф.уравнения

A=[ 0, 1, 0;

    0, 0, 1;

    -1/a(1), -a(3)/a(1), -a(2)/a(1)];

B=[0; 0; 10/a(1)];

Fxt=A*Xk+B;

Выводы и анализ результатов

Выполняя процедуру последовательно для n = 5, 10, 20, 40, 50, получим графики решений ДУ.

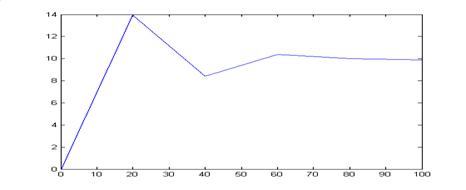
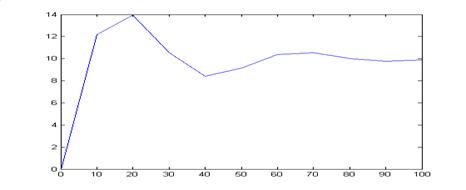
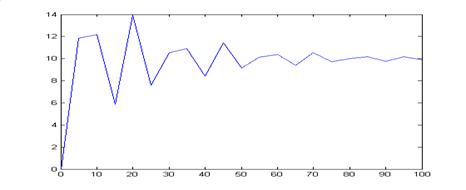
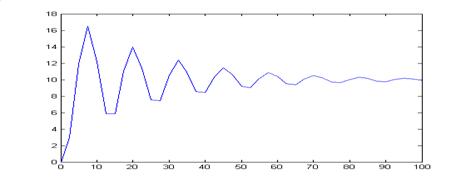
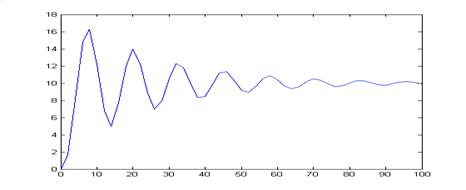
Выполняя процедуру последовательно для n = 5, 10, 20, 40, 50, получим графики погрешностей.

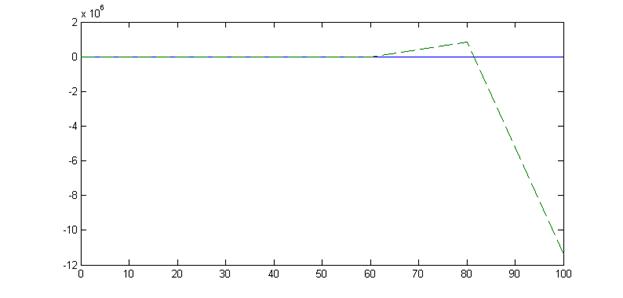
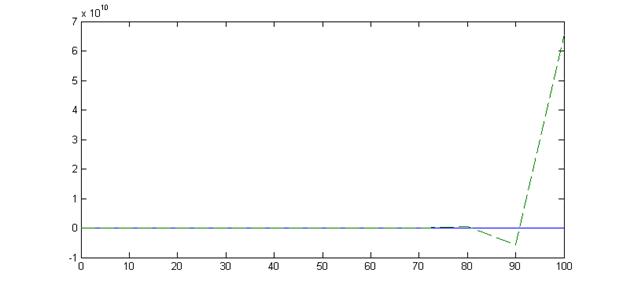
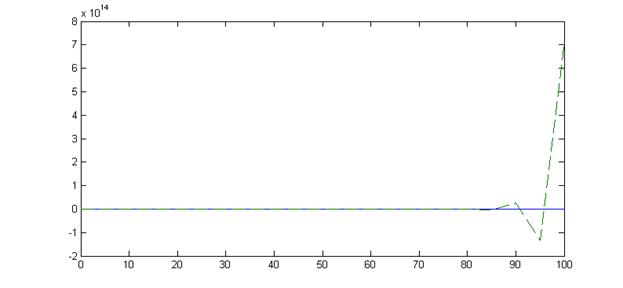
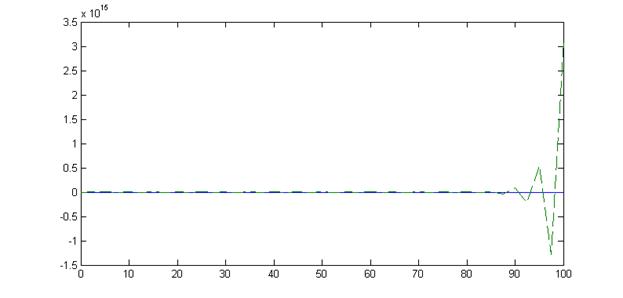
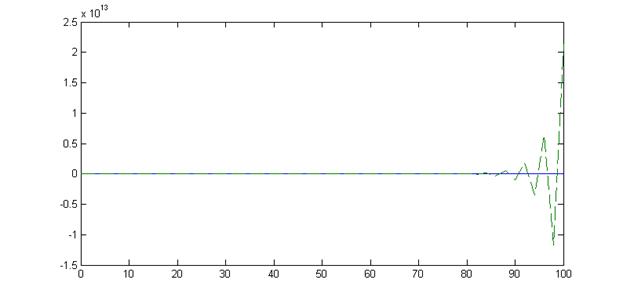
На представленных графиках сплошная линия соответствует погрешности решения сольвера Matlab, штриховая – погрешности решения методом Адамса-Бэшфорта.

На графиках видно, что метод Адамса-Бэшфорта расходится на конце интервала интегрирования. С увеличением количества шагов вдвое, а значит, уменьшением величины шага, амплитуда колебаний увеличивается, причем она также увеличивается со временем.

Таким образом, при равномерном выборе величины шага метод Адамса-Бэшфорта 2го порядка явлеяется недостаточно устойчивым. Точности решения можно добиться, если корректировать величину шага с течением времени сообразно с требованиями устойчивости.

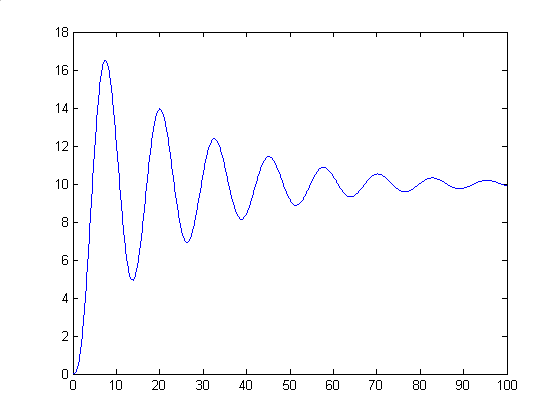
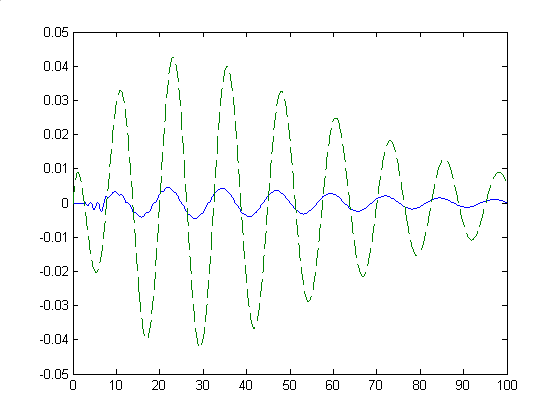
Графики решения и погрешности при n=1000: