






























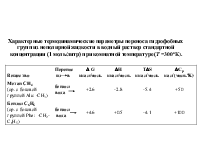





Лекции 2-3 Молекулярные силы в биологических структурах
Основы теории межмолекулярных взаимодействий
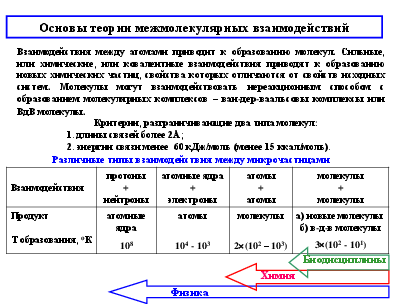
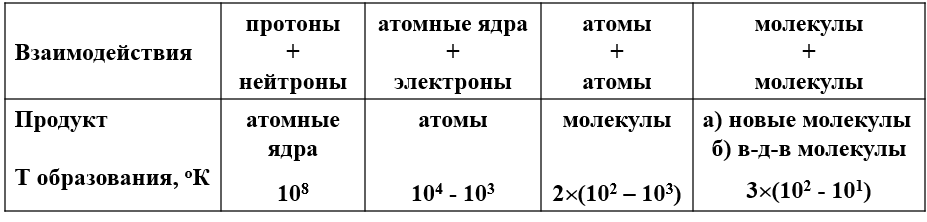
Взаимодействия между атомами приводит к образованию молекул. Сильные, или химические, или ковалентные взаимодействия приводят к образованию новых химических частиц, свойства которых отличаются от свойств исходных систем. Молекулы могут взаимодействовать нереакционным способом с образованием молекулярных комплексов – ван-дер-ваальсовы комплексы или ВдВ молекулы.
Критерии, разграничивающие два типа молекул: 1. длины связей более 2Å; 2. энергии связи менее 60 кДж/моль (менее 15 ккал/моль).
Различные типы взаимодействия между микрочастицами
Биодисциплины
Химия
Физика
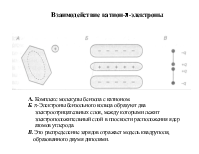
Ван-дер-ваальсовые (ВВ) силы. ВВ силы играют важнейшую роль в образовании конденсированных жидких и твёрдых состояний. Ими определяются взаимодействия газов и возникающие отклонения законов идеальных газов.
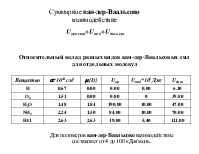
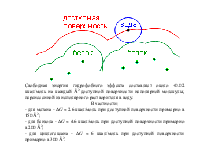
Биомакромолекулы можно рассматривать как своего рода конденсируемые системы, состояния которых определяются относительно слабых невалентных взаимодействий. Именно такие взаимодействия дают основной вклад к стабилизации конденсации состояния биополимеров и его изменения в процессе функционирования. Значения энергии при ВВ взаимодействиях лежат в интервале 4-8 кДж/моль и выше. Энергия при комнатной (температуре) составляет 2,5 кДж/моль, а энергия коллективных ионных связей составляет 150 - 600 кДж/моль. координата реакции
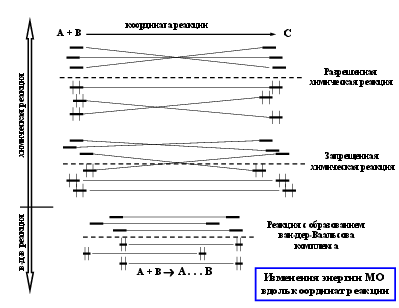
А + В
С
Разрешенная химическая реакция химическая реакция
Запрещенная химическая реакция
Реакция с образованием ван-дер-Ваальсова комплекса в-д-в реакция
Изменения энергии МО вдоль координат реакции
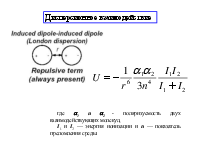
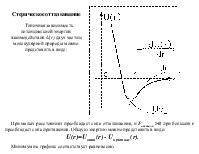
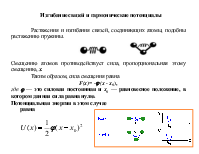
Теория межмолекулярного взаимодействия описывает зависимость энергии взаимодействия от расстояния между молекулами и их взаимной ориентацией в окрестностях минимума (вблизи положения равновесия)
Все межмолекулярные силы имеют электростатическую природу. Их разделяют на короткодействующие и дальнодействующие Короткодействующие убывают экспоненциально с ростом r: e-r. Они возникают в результате перекрывания электронных волновых функций, описывающих состояние отдельных молекул Дальнодействующие силы изменяются на больших расстояниях по закону r-n, n – целое, положительное
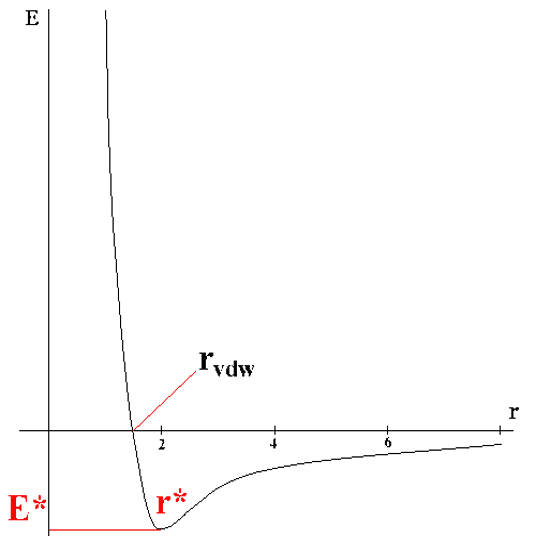
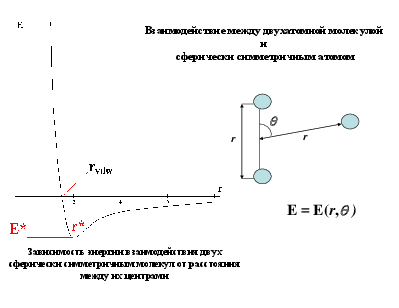
Взаимодействие между двухатомной молекулой и сферически симметричным атомом
r
r
E = E(r, )
Зависимость энергии взаимодействия двух сферически симметричным молекул от расстояния между их центрами
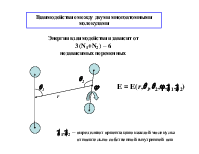
Взаимодействие между двумя многоатомными молекулами
Энергия взаимодействия зависит от 3(N1+N2) – 6 независимых переменных
2
E = E(r,1,2,,1,2)
1
r
1,2 – определяют ориентацию каждой молекулы относительно собственной внутренней оси
Электростатические взаимодействия
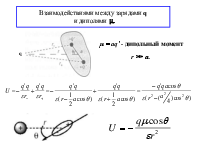
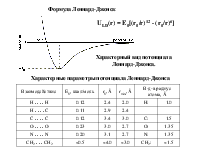
Взаимодействия между электрическими мультиполями называются электростатическими взаимодействиями. Результирующая величина электростатического взаимодействия определяется суммой вкладов, обусловленных взаимодействиями между различными мультиполями: EES = qRqT/r + qR T/r2 +...+ R T/r3 +...+ QRQT/r5 +... где: монополь q (заряд), дипольный момент , квадрупольный момент Q систем R или T.
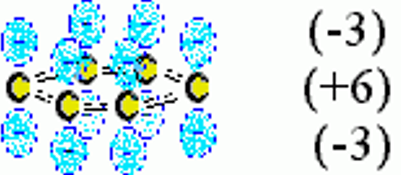
квадруполь
Взаимодействиями между монополями q (зарядами)
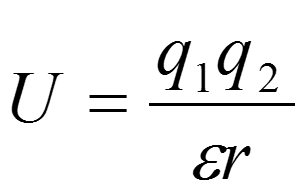
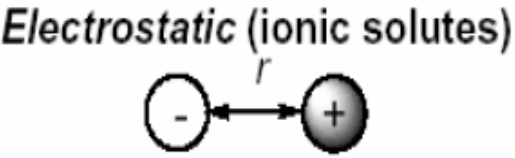
Термодинамика электростатических взаимодействий
Энергия электростатических взаимодействий эквивалентна работе, необходимой для перемещения зарядов в соответствующие позиции при постоянных значениях температуры и давления. Отсюда следует, что это свободная энергия, а не просто потенциальная энергия, равная энтальпии. При более точном анализе кулоновского потенциала оказывается, что в воде он обусловлен энтропией.
Чтобы разложить электростатический потенциал на H и S запишем формулу для энтропии S = -дG/дТ, где G — потенциальная энергия, определяемая по закону Кулона.
Дифференцируя это выражение, получаем
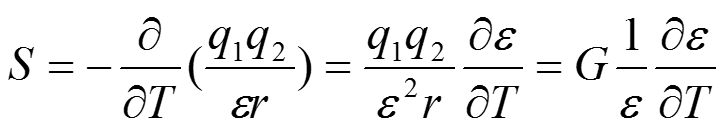
Если диэлектрическая проницаемость не изменяется с изменением температуры, энтропия должна быть равна нулю
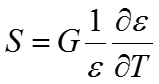
и кулоновский потенциал должен быть эквивалентен энтальпии.
Но диэлектрическая проницаемость воды сильно зависит от температуры; ее снижение составляет 0,46% в расчете на градус Кельвина. Это означает, что = -0,0046 и S = -0,0046G. При Т = 300 К величина ТS = -1,38G. Таким образом, вклад энтропии в потенциальную энергию электростатического взаимодействия выше, чем собственно величина свободной энергии.
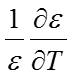
Собственная электростатическая энергия
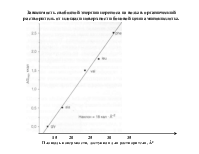
Энергию внедрения иона в диэлектрическую среду можно рассчитать из кулоновского потенциала следующим образом. Рассмотрим работу, которую необходимо совершить, чтобы произошло небольшое приращение заряда, q’, на поверхности сферы радиусом r, несущей заряд q’
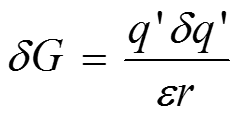
Интегрируем, начиная с заряда, равного нулю, и заканчивая величиной q
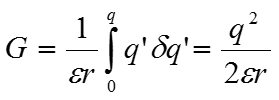
Эту энергию называют собственной энергией заряда или энергией Борна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.