Молекулярные силы в биологических структурах. Основы теории межмолекулярных взаимодействий, страница 2

Можно рассчитать свободную энергию внедрения иона в растворитель данной диэлектрической проницаемости. В случае воды это энергия гидратации. Величина энтальпии гидратации позволяет судить о гидратации как процессе поляризации окружающей воды. Чтобы вычислить энтальпию из уравнения Борна, необходимо продифференцировать его по температуре, получив в результате величину -S, и рассчитать Н как G + TS. Вычисленная таким образом энтальпия обратно пропорциональна расстоянию, r, и это подтверждают экспериментальные данные

-60

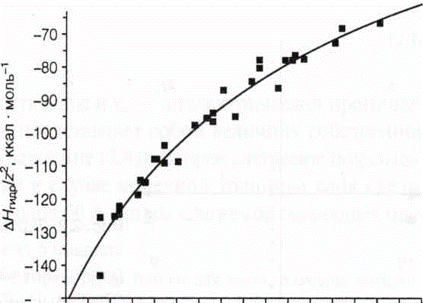
Зависимость энтальпии гидратации от расстояния. Представлена величина энтальпии для различных ионов, деленная на q2. Эта обратная зависимость от расстояния описывается уравнением Борна. Сплошная кривая соответствует пропорциональности -1/r

150

0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 r,Å

Сила отображения Сильная зависимость собственной энергии от диэлектрической проницаемости среды означает, что вблизи границы раздела двух сред, различных по диэлектрической проницаемости, заряд будет притягиваться к области более высокой диэлектрической проницаемости. Этот ион будет оказывать более сильное поляризующее действие на данную область, и образовавшиеся в ней диполи будут притягивать ион к границе раздела фаз. Подобно этому, ион в высокодиэлектрической среде будет отталкиваться от соседней среды с низким значением .

При 2 > 1 заряд в точке отображения имеет величину q’ = -q(2 - 1)/(2 +1). По закону Кулона, потенциальная энергия взаимодействия зарядов q и q’, разделенных расстоянием 2r, равна

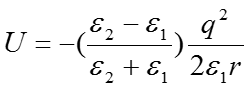
Таким образом, сила действия диэлектрической среды на заряд имеет ту же форму, что сила действия другого заряда. Знак «-» в этом уравнении означает, что сила направлена в сторону области с более высоким значением . При 2 > 1, сила, действующая на ион, направлена вправо.

• Чтобы выяснить, как сила отображения влияет на энергетику некоторых биологических процессов, рассмотрим два важных случая.
• заряд расположен в середине пластины конечной толщины с низкой
• , окруженной на бесконечном расстоянии с обеих сторон средой с
• высокой .
• В случае диэлектрической пластины свободная энергия
• внедрения заряда q в ее центр описывается выражением

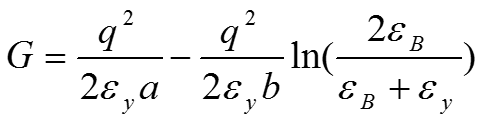
У

B

В

а

q

b

Заряд расположен в центре сферы с низкой , окруженной средой с высокой .

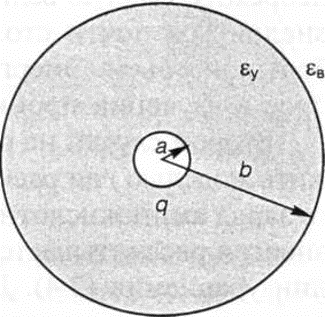
Движение каждого элемента заряда q’ к поверхности при r = а можно разделить на два этапа: — движение через воду к поверхности при r = b, когда работа равна , — движение через углеводород к поверхности при r = а, когда работа равна

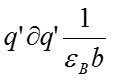
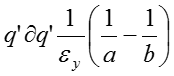
Интегрирование по q' от нуля до q позволяет получить выражение

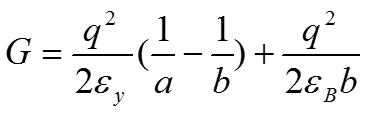
Эти расчеты показывают, что внедрение заряда в середину липидной мембраны (1 случай) или во внутреннюю область глобулярного белка (2 случай) почти так же затруднено, как внедрение его в большой объем среды с подобной низкой .

При наличии свободных зарядов (например, соли) в воде, электростатические взаимодействия ослабевают с расстоянием r не по закону (1/r), а по экспоненте: (1/r) x exp(-r/D). Здесь D - радиус Дебая-Хюккеля, он соответствует характерному размеру противоионного облака вокруг заряда. Величина D не зависит от самого заряда, а зависит от концентрации ионов в среде ci , от диэлектрической проницаемости среды  и температуры Т. В воде, при комнатной температуре, D  3/I1/2Å, где I = 1/2 i ci zi2 - ионная сила раствора в моль/литр. Сумма берется по всем сортам ионов в растворе, zi  - заряд (в единицах протонного заряда), ci  - концентрация (в моль/литр) иона i. Обычным физиологическим условиям соответствует I  0.1-0.15 моль/л; при этом D  8Å.

Взаимодействиями между зарядами q и диполями 

µ = aq’ - дипольный момент

r >> а

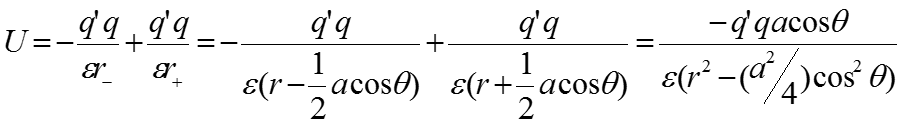
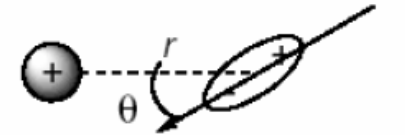
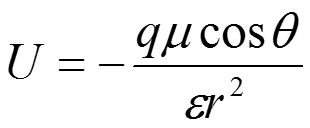
Если диполь поместить непосредственно рядом с зарядом q, величина  будет равна нулю и выражение для энергии взаимодействия приобретет вид