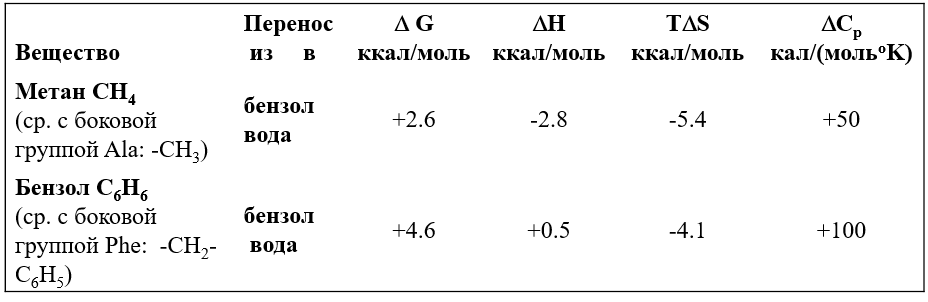
Характерные термодинамические параметры переноса гидрофобных групп из неполярной жидкости в водный раствор стандартной концентрации (1 моль/литр) при комнатной температуре (T =300oK).
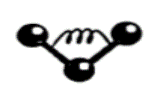
Изгибание связей и гармонические потенциалы
Растяжения и изгибания связей, соединяющих атомы, подобны растяжению пружины. Смещению атомов противодействует сила, пропорциональная этому смещению, х. Таким образом, сила смещения равна F(x)= - (x - x0), где — это силовая постоянная и x0 — равновесное положение, в котором данная сила равна нулю. Потенциальная энергия в этом случае равна

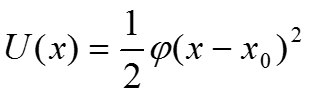
При подстановке выражения для потенциальной энергии и соответствующей силы смещения F(x) = -(x - x0) в уравнение Ньютона для движения атомов получаем выражение для классического гармонического осциллятора Решение получаемого таким способом уравнения представляет собой периодическую синусоидальную или косинусоидальную функцию с частотой (/m). Это частота колебаний связи, и для определения силовых постоянных используются данные, получаемые с помощью колебательной спектроскопии.
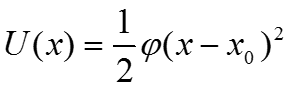
![]()
В случае С—С-связи силовая постоянная растяжения равна 5•105 дин•см-1, или 660 ккал•Å-2•моль-1. Эта величина означает, что энергия смещения связи всего на 0,1Å превысит тепловую энергию при комнатной температуре. Силовые постоянные растяжения многих ковалентных связей совпадают по порядку величин с этой постоянной для С—С-связи, и соответственно растяжение связей не может быть существенным фактором пластичности молекул. Силовые постоянные изгибания связей, как правило, примерно в 10 раз ниже, и тепловая энергия может обусловливать деформацию примерно на 0,2Å. Типичная силовая постоянная для растяжения водородной связи составляет примерно 30 ккал•Å-2 •моль-1. Хотя каждая из этих степеней свободы в отдельности не существенна для пластичности молекул, эффекты многих таких движений в крупной макромолекуле могут складываться, обеспечивая ее значительную гибкость.
Можно представить функцию потенциальной энергии вблизи минимума в форме суммы слагаемых, идентичных выражению для гармонического осциллятора.
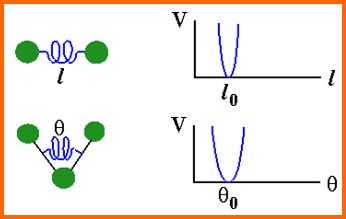
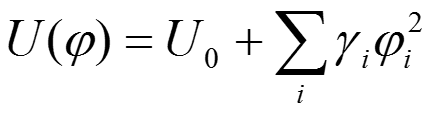
Если это выражение для потенциальной энергии подставить в уравнение для движения атомов, можно определить моды колебательного движения сложной молекулы. Их называют нормальными модами или нормальными колебаниями молекулы. Фактически в многоатомной молекуле это именно моды, а не частоты колебаний индивидуальных связей. Функция потенциальной энергии также имеет нормальные моды, что позволяет выразить гибкость молекулы через сумму деформаций.
Можно представить функцию потенциальной энергии вблизи минимума в форме суммы слагаемых, идентичных выражению для гармонического осциллятора.

Если это выражение для потенциальной энергии подставить в уравнение для движения атомов, можно определить моды колебательного движения сложной молекулы. Их называют нормальными модами или нормальными колебаниями молекулы. Фактически в многоатомной молекуле это моды, измеряемые с помощью колебательной спектроскопии, а не частоты колебаний индивидуальных связей. Функция потенциальной энергии также имеет нормальные моды, и это помогает выразить гибкость молекулы через сумму деформаций.
Анализ гармонического потенциала в рамках статистической механики позволяет с помощью классического конфигурационного интеграла
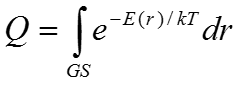
где r – вектор, определяющий позиции всех атомов, E(r) – потенциальная энергия молекулы как функция этих положений, GS – диапазон интегрирования, который характеризует макросостояние путем ограничения пространства координат
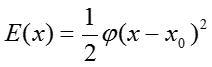
При подстановке в него выражение для потенциальной энергии в виде
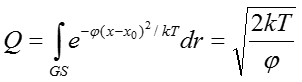
получим
И свободная энергия определяется как
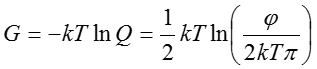
Таким образом, при возрастании силовой постоянной повышается свободная энергия. Это отражает уменьшение энтропии в результате ограничения х меньшей областью значений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.