Интерполирование функции для заданных полиномов

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Системного Анализа и Управления

Курсовая работа

Курс: «Вычислительная математика»

Тема: «Интерполирование функции »

Выполнил:  ст. гр. 2082/1

                                                                                                   Андреенко Д.А.         

                                                                                      Проверил:

                                                                                                 Кирсяев А.Н.

Санкт-Петербург

2006

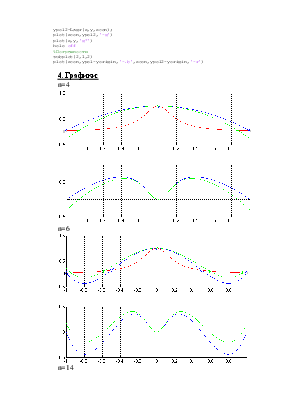
Сравнить графики заданной функции f(x) и интерполяционных полиномов Pn(x) для n=2, 6, 14 на интервале x=[c,d] при двух вариантах выбора узлов:

1. равномерно, с шагом h=(d-c)/n.
2. по Чебышеву.

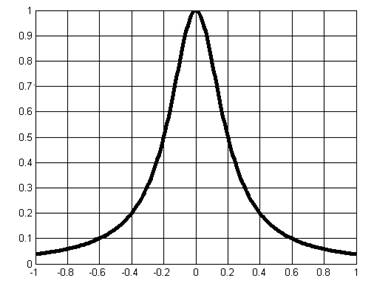
11 вариант, формула Лагранжа.

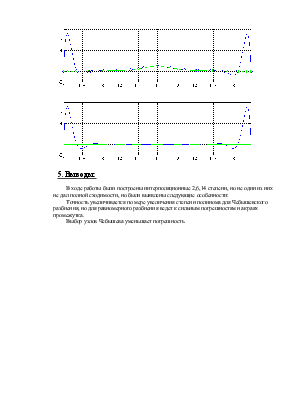
По результатам работы должны быть построены графики – исходной функции, интерполяционных полиномов 2, 6, 14 степени точности, погрешности полиномов относительно исходной функции.

2. Теоретическая часть:

Данная задача делится на несколько основных частей:

a.  Выбор узлов для интерполяционного полинома на отрезке

В данной работе предложено два варианта – равномерное и Чебышевское разбиение.

Равномерное - x(i)=a+h*(i-1), где h=(d-c)/n;

i- итерационная переменная,

h – шаг разбиения зависящий от длины отрезка [c,d] и количества узлов разбиения n.

Чебышевское - x(i)=1/2*((a-b)*cos((2*i-1)*pi/(2*n+2))+a+b), где

i - итерационная переменная,

отрезок [a,b], количества узлов разбиения n.

b.  Вычисление значений функции в этих узлах

Исходная функция была задана в кусочно-линейной форме, и в зависимости от аргумента возвращала необходимое значение.