Интерполирование функции для заданных полиномов, страница 3

%*****n=6*****

a=-1;%Predefined constants

b=1;

buildstep=0.01;

n=6;

%RR

x=RR(a,b,n);

y=OP(x);

xcon=[a:buildstep:b];

yorigin=OP(xcon);

ypol=Lagr(x,y,xcon);

figure('Name','n=6 | Lagrange');

subplot(2,1,1)

hold on

plot(xcon,yorigin,'-.r',xcon,ypol,'-b')

plot(x,y,'bo')

%CHR

x=CHR(a,b,n);

y=OP(x);

ypol2=Lagr(x,y,xcon);

plot(xcon,ypol2,'-g')

plot(x,y,'g*')

hold off

%Погрешности

subplot(2,1,2)

plot(xcon,ypol-yorigin,'-.b',xcon,ypol2-yorigin,'-r')

%*****n=14*****

a=-1;%Predefined constants

b=1;

buildstep=0.01;

n=14;

%RR

x=RR(a,b,n);

y=OP(x);

xcon=[a:buildstep:b];

yorigin=OP(xcon);

ypol=Lagr(x,y,xcon);

figure('Name','n=14 | Lagrange');

subplot(2,1,1)

hold on

plot(xcon,yorigin,'-.r',xcon,ypol,'-b')

plot(x,y,'bo')

%CHR

x=CHR(a,b,n);

y=OP(x);

ypol2=Lagr(x,y,xcon);

plot(xcon,ypol2,'-g')

plot(x,y,'g*')

hold off

%Погрешности

subplot(2,1,2)

plot(xcon,ypol-yorigin,'-.b',xcon,ypol2-yorigin,'-r')

4. Графики:

n=4

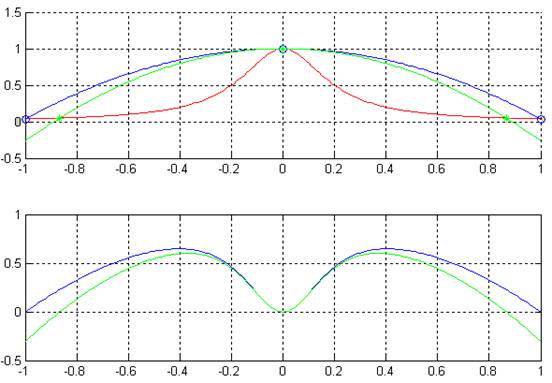
n=6

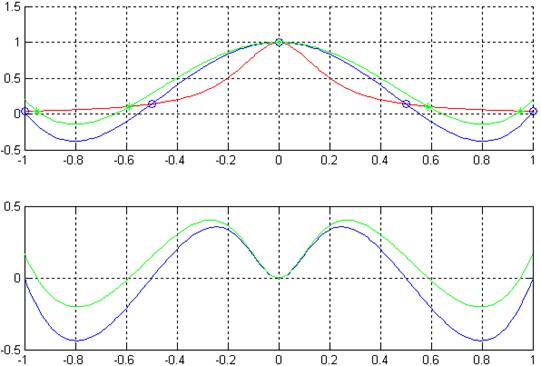
n=14

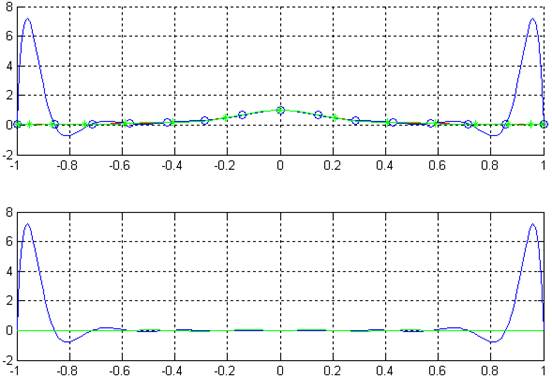
5. Выводы:

В ходе работы были построены интерполяционные 2,6,14 степени, но не один из них не дал полной сходимости, но были выявлены следующие особенности:

Точность увеличивается по мере увеличения степени полинома для Чебышевского разбиения, но для равномерного разбиения ведет к сильным погрешностям на краях промежутка.

Выбор узлов Чебышева уменьшает погрешность