Линейное программирование (Расчет питательности рациона скота, состоящего из комбикорма трех видов)

Министерство образования Российской Федерации

Санкт-Петербургский колледж Морского Приборостроения

Курсовая работа

По предмету: «Математические методы»

Тема: «Линейное программирование»

Специальность 2203, группа М-343

Выполнил студент:

А

Проверил преподаватель:

Оценка__________

Подпись_________

2006

Оглавление

1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ_ 3

1.1 Постановка задачи_ 3

1.2 Решение симплекс-методом_ 4

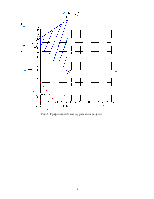
2 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ Л.П. 8

3 ТРАНСПОРТНАЯ ЗАДАЧА_ 10

3.1 Нахождение начального плана транспортной задачи_ 10

3.2 Метод Северо-Западного угла 10

4 ЗАКЛЮЧЕНИЕ_ 14

1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

1.1 Постановка задачи

Для кормления скота требуется составить суточный рацион, обладающий определенной питательностью, а именно он должен содержать не более b1 единиц биостимуляторов, ровно b2 единиц микроэлементов и не менее b3 кормовых единиц. Вещества, входящие в рацион, не могут быть получены в чистом виде. Они содержатся в комбикормах трех видов. Известно, что в одном кГ комбикорма каждого вида содержится соответственно aij единиц каждого питательного вещества. Известна себестоимость cij одного кГ комбикорма каждого вида или его калорийность dij.

Требуется определить, сколько кГ комбикорма каждого вида нужно взять для составления суточного рациона, чтобы он удовлетворял условиям питательности и имел бы наибольшую калорийность.

При решении задач такого вида возникают следующие этапы:

1.   Идентификация переменных:

х1 - комбикорм 1 вида х2 - комбикорм 2 вида х3 - комбикорм 3 вида

2.  Определение целевой функции Функция наибольшей калорийности:

f = 3x1+6x2+7х3 => max

3.  Определение ограничений задачи:

a) Биостимуляторы

x1+2x2+6х3≤42

b) Микроэлементы

6x1+8x2 +10х3=136

с) Кормовые единицы

6x1+2x2 +х3≥88

Математическая модель:

f = 3x1+6x2+7х3 => max

 x1+2x2+6х3≤42

6x1+8x2 +10х3=136

6x1+2x2 +х3≥88

Линейный характер модели состоит в том, что и целевая функция и ограничения носят линейный характер, т.е переменные в первой степени.

1.2 Решение симплекс-методом

В данной задаче ограничения представляют собой  неравенства по смыслу «≥», следовательно, в этом случае прибегают к двухэтапному симплекс-методу.

I этап представляет решение задачи с новой целевой функцией φ, которая минимизируется (φ →min). В качестве переменных в функцию φ  входят переменные искусственного базиса φ = Z1+Z2→min.

f = 3x1+6x2 +7х3→ max

x1+2x2+6х3≤42                 x1+2x2+6х3+s1= 42

6x1+8x2 +10х3=136                       6x1+8x2 +10х3+z1 = 136

6x1+2x2 +х3≥88                              6x1+2x2 +х3 - s2+z2 =88

х1,х2,х3≥0                                          х1,х2,х3≥0 ; z1,z2≥ 0                                                   

φ = Z1+Z2→min

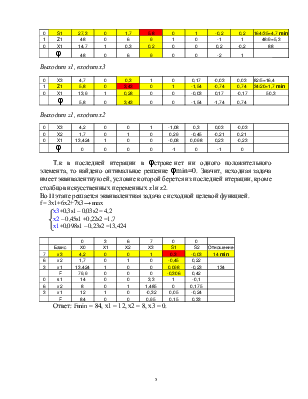
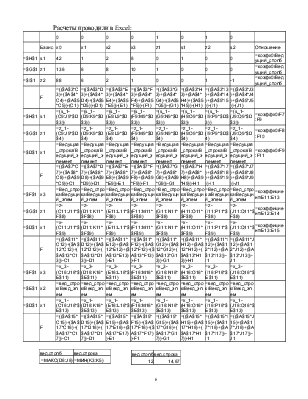
Перед началом решения в ограничениях необходимо выделить базисные переменные, т.е. такие, которые входят только в одно уравнение с коэффициентом «1».Вычисления сводятся в таблицы.

Выходит z2, входит х1.

В строке целевой функции выбирается максимально положительный коэффициент. Этот коэффициент определяет ведущий столбец.

Составляется отношение коэффициентов столбца Хо к соответствующим коэффициентам ведущего столбца, кроме нулевых и отрицательных, получившееся отношение записывается в столбец «Отношение».

Из получившихся отношений выбирают минимальную величину. Это будет соответствовать ведущей строке. В случаи равенства выбирается любая.