Прикладные математические методы: Методические указания к практическим занятиям (Простейшие оценки надежности. Вероятностные характеристики надежности. Проверка достоверности гипотезы о законе распределения)

разрешается произвольно  принять гипотезу о законе распределения:

а) Гипотеза 1. Суммарный ущерб от каждой категории аварий одинаков, т.е.  крупная авария + 10 средних аварий + 100 мелких аварий, или 111 авариям соответствует ущерб 300000 у.е. Средний ущерб от одной аварии при этом предположении

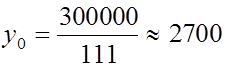у.е.

 у.е.

б) Гипотеза 2. Число аварий каждой категории одинаково, т.е.

у.е.

Средний ущерб от одной аварии

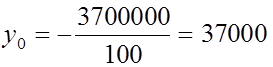у.е.

2. Ввиду большого расхождения результатов оценки по гипотезам 1 и 2 необходимо получить дополнительную информацию для уточнения закона распределения аварий по категориям. Эта информация может быть получена от других энергосистем с приведением к собственным условиям или обработкой результатов так называемой «малой выборки», т. е. по произвольно отобранному малому числу аварий.

Пример 4. Характеристики надежности в классификации.

Трансформатор районной подстанции по своему назначению и сложности относится к 3 классу надежности, 1 группе надежности. По ГОСТ он должен характеризоваться

1.  средней наработкой на отказ - ;

2.  средней наработкой до первого отказа - ;

3.  ресурсом до капитального ремонта - ;

4.  средним временем восстановления - ;

5.  средними трудозатратами на аварийное восстановление - W ;

6.  коэффициентом технического использования - .

Примечание: предлагается определить примерный перечень показателей надежности для какого-либо конкретного изделия, численные показатели его, сопоставить показатели изделий разных типов.

Пример 5. Испытания на надежность.

Определить   число   дизель-генераторов   аварийного   электроснабжения, которые необходимо поставить на испытания. Вероятность безотказной работы Р = 0,9 за время ликвидации аварии t = 240 часов. Эта вероятность в ходе испытаний определяется с доверительной вероятностью .

Если считать, что закон распределения наработки на отказ неизвестен, то:

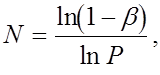
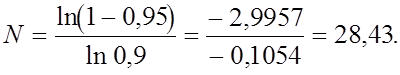
Вывод: на испытания в течение 240 часов необходимо поставить 30 генераторов. Если за время испытаний не произойдет ни одного отказа, то требуемая вероятность обеспечивается.

Приближенная точечная оценка вероятности безотказной работы при нескольких отказах т, предположим т = 1, можно определить по формуле:

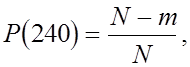
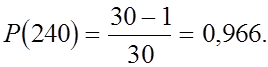
Это противоречит результатам, приведенным выше. Очевидно, что точечная  оценка должна применяться для  оборудования  и  схем более низкой вероятности отказа.

Пример 6. Распознавание и оценка надежности «тренда».

Снята экспериментальная зависимость между мощностью  и расходом топлива агрегата . Необходимо подобрать аппроксимационную кривую.

i	1	2	3	4	5	6	7
	140	150	160	170	180	190	200
	37,0	37,0	41,0	44,0	43,0	47,0	52,0

1. Линейная аппроксимация:

.

Принятие в качестве критерия минимума среднеквадратической ошибки на интервале позволяет определить систему уравнений для коэффициентов а и в:

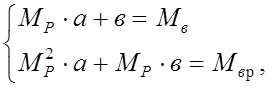
где

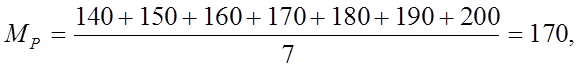
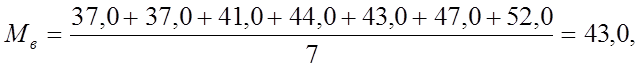
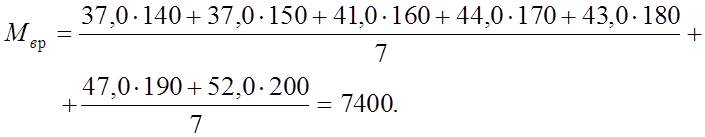
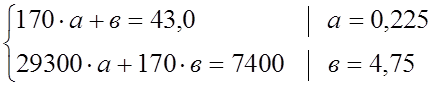
i	1	2	3	4	5	6	7
	140	150	160	170	180	190	200
	37,0	37,0	41.0	44,0	43,0	47,0	52,0
В	36,25	38,5	40,75	43,0	45,25	47,5	49,75
	-0,75	+1,5	-0.25	-1,0	+2,25	+0,5	-2,25

 или

 - принятая аппроксимация достоверна.

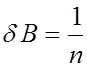
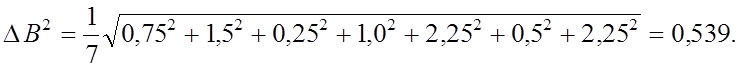
2.  Аппроксимация кривой второго порядка

При тех же предположениях система уравнений для определения коэффициентов параболы имеет вид:

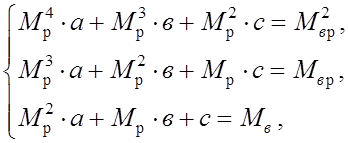
где

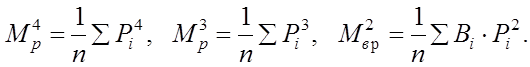
Аналогично варианту 1:

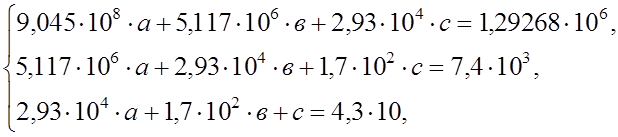
i	1	2	3	4	5	6	7
	140	150	160	170	180	190	200
	37,0	37,0	41,0	44,0	43,0	47,0	52,0
В	40,2	38,5	38,3	39,7	42,8	47,5	53,8
	+3,2	+1,5	-2,7	-4,3	-0,2	+0,5	+1,8

 или

Принятая аппроксимация достоверна.

Вопрос об использовании варианта № 1 или варианта № 2 должен решаться с учетом дополнительных факторов.

Примечание.

Если бы  варианта № 2 было отмечено при , то:

и аппроксимация должна считаться недостоверной.

Пример 7. Проверка достоверности гипотезы о законе распределения

Проверить достоверность гипотезы о законе распределения отказов выключателя по результатам испытаний:

i	1	2	3	4	5	6
, час	91	143	167	200	250	1000
	1	1	1	2	1	1

т - число отказов.

Общее число отказов:

Средняя наработка на отказ:

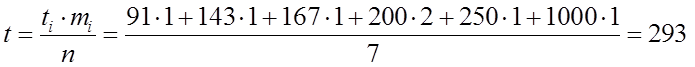час.

Средняя частота отказов:

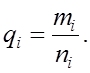
Экспериментальная функция распределения:

i	I	2	3	4	5	6
	0,143	0,143	0,143	0,286	0.143	0,143
F	0,143	0,286	0,429	0,715	0,858	1,000

Переведем время в относительное:

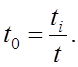
Функция распределения при экспоненциальном законе распределения:

i	1	2	3	4	5	6
t0	0,310	0,488	0,570	0,682	0,853	3,413
	0,265	0,385	0,435	0,495	0,575	0,965

Расхождение, между экспериментальными значениями и значениями по экспоненциальному закону распределения:

i	1	2	3	4	5	6
D	0,122	0,099	0,006	0,220	0,283	0,0035

Максимальному отклонению D = 0,283 при 7 наблюдениях соответствует

Для У = 0,75 по критерию Колмогорова .

Вероятность достаточно велика, чтобы считать отклонение случайным, а гипотезу об экспоненциальным законе распределения не противоречащей результатам испытаний, если пренебречь в учебных целях положением Колмогорова о необходимости не менее 100 экспериментальных точек для применения критерия.

Примечание.

Если внимательно посмотреть на распределение отказов по шкале времени, то видно, что подавляющее большинство отказов располагается в пределах первой четверти. Это соответствует скорее зоне приработки,. чем работе с постоянным потоком отказов, т.е. эксперимент проведен некорректно, необходимо продолжить исследования.

Пример 8. Использование метода факторного анализа для определения параметров модели действующих факторов

Принято считать, что надежность воздушных выключателей зависит от следующих факторов.

1. Перенапряжения и электрическая прочность загрязненной изоляции. Верхний уровень - кратность перенапряжений - 2.

Нижний уровень - кратность перенапряжений -1,3.

2. Отключаемый ток короткого замыкания.

Верхний уровень - 100% предельного тока отключения.

Нижний уровень - 60% и менее.

3. Длительность воздействия максимальных температур.

Верхний уровень - +40 °С в течение 30 дней в год и более. Нижний уровень - +40 °С в течение 10 дней и менее.

4. Длительность воздействия минимальных температур,

Верхний уровень - -40 °С в течение 30 дней в год и более. Нижний уровень - -40 °С в течение 10 дней и менее.

5. Число отключении КЗ в течение года.

Верхний уровень-10 и более.

Нижний уровень -1 и менее.

6. Число оперативных переключений.

Верхний уровень - 200 в год.

Нижний уровень - 12 и менее в год.

По плану факторного эксперимента для выключателей серии ВВН были получены следующие результаты:

К	т	S	l	l 1	l 2
		год	год -1	год -1	год -1
1	4	71	0,056	0,0609	0,0641
2	9	289	0,031	0,0267	0.0283
3	3	40	0,050	0,0439	0,0423
4	1	34	0,029	0,0349	0,0317
5	1	50	0,020	0,0169	0,0201
6	7	287	0,024	0,0295	0,0311
7	1	98	0,012	0,0188	0,0171
8	2	32	0,062	0,0562	0,0529

Полином регрессии по результатам эксперимента имеет вид: