Прикладные математические методы: Конспекты лекций (краткий курс)

подставляются значения неизвестных, найденные на предыдущей итерации . В результате их подстановки в первое уравнение системы (11.2) сразу определяется следующее, более уточненное, значение первой неизвестной . Если при определении второй переменной  в правую часть второго уравнения системы (2.2) подставить вместо  значение , то можно ожидать, что  будет найдено с более высокой точностью.

Данный принцип нашел применение в так называемом методе Зейделя. В отличие от метода простой итерации для вычисления i-й переменной на каждом k-м. шаге итерационного процесса используются значения переменных, вычисленные как на предыдущем (k—1)-м шаге, так и на данном. При этом на k-м. шаге итерационного процесса система уравнений имеет вид:

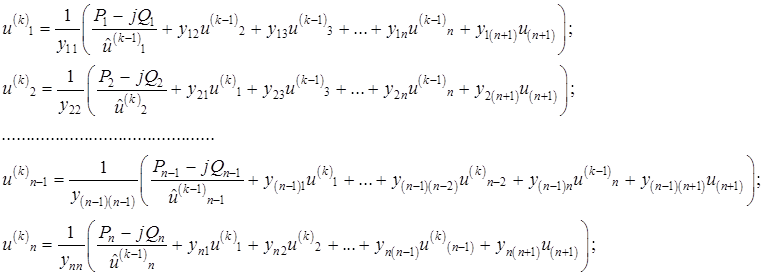
Метод Зейделя обычно характеризуется более быстрой сходимостью по сравнению с методом простой итерации, поэтому метод простой итерации не нашел применения в практике расчетов установившихся режимов электрических систем.

3. Основы матричной алгебры

3.1. Основные определения

Расчеты режимов реальных ЭЭС практически невозможно осуществить без применения ЭВМ. Поэтому важным вопросом является представление приведенных выше систем уравнений в виде, пригодном для использования вычислительной техники. Для этого применяется так называемое матричное представление, когда системы уравнений описываются специальными матрицами. Правила операций с матрицами определяются матричной алгеброй.

Матрица – таблица величин, обладающих каким-либо общим признаком и записанных в определенной последовательности.

Например в системе узловых уравнений (2.1) напряжения узлов , , ,  являются неизвестными, а мощности P и Q и напряжение в балансирующем узле  - заданные параметры режима схемы.

Можно выделить матрицу коэффициентов при неизвестных напряжениях, которая условно обозначается .

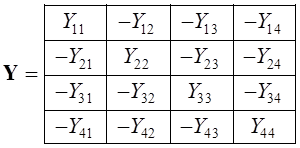
Входящие в матрицы элементы нумеруются двумя индексами: первый индекс соответствует номеру строки, а второй – номеру столбца. Например, пусть имеется матрица А.

Ее элементы могут быть обозначены следующим образом:

Матрица называется квадратной, если число ее строк равно числу столбцов. Матрица А является квадратной.

Квадратная матрица называется диагональной, если все ее элементы вне главной диагонали равны нулю.

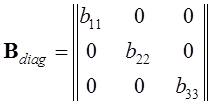
Диагональная матрица, все элементы которой на главной диагонали равны нулю, называется единичной.

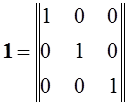
Матрица, все элементы которой равны нулю, называется нулевой и обозначается символом .

Матрица, содержащая один столбец, называется матрицей-столбцом или вектором, а содержащая одну строку – матрицей-строкой. Например, совокупность искомых неизвестных напряжений и заданных параметров режима схемы в системе узловых уравнений (2.1) могут быть представлены векторами и :

Две матрицы считаются равными, если равны их элементы с одинаковыми индексами. Пример две матрицы A и B:

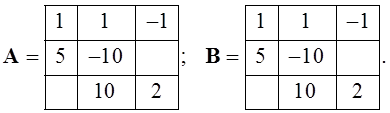
Если строки матрицы  записать в виде столбцов, то получится транспонированная матрица , где индекс  означает транспонирование. Очевидно, что для строки транспонированной матрицей является столбец, а для столбца – строка. Для рассмотренных выше матриц:

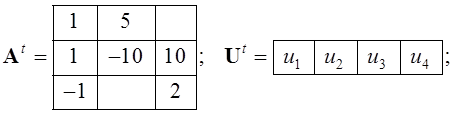
Квадратная матрица называется симметричной относительно главной диагонали, если равны между собой ее недиагональные элементы, расположенные в противоположных ячейках относительно главной диагонали . Симметричная относительно главной диагонали матрица совпадает с транспонированной.

3.2. Алгебраические действия над матрицами

Алгебра матриц позволяет оперировать одновременно с целыми группами однотипных величин и записывать символически производимые над ними действия в форме, аналогичной действиям над обычными числами.

Сложение (вычитание) матриц есть действие, заключающееся в составлении