Методические указания к практическим занятиям по курсу «Прикладные математические методы» (Определение необходимого объема испытаний. Расчет оптимального распределения активной мощности в теплоэнергетической системе)

РАЗДЕЛ 1

ВВЕДЕНИЕ

Создание новых машин, аппаратов и комплексов требует применения таких методов анализа, которые позволяли бы при проектировании объективно учесть опыт эксплуатации, данные экспериментов.

Эксплуатация и испытания позволяют провести проверку методов и моделей и тем самым  повысить надежность. Студенты и молодые специалисты должны уметь выносить суждение и обосновывать его точность и надежность по сравнительно небольшому объему опытных данных.

ЗАДАЧА 1.1

Определение необходимого объема испытаний

В основе всех методов лежит закон Бернулли, формулируемый следующим образом:

Для независимых событий расхождение между частостью события  и вероятностью  при увеличении  становится меньше малой величины

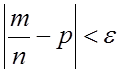
Количественные соотношения можно вывести на основании дополнения к теории Бернулли, выведенного П.Л.Чебышевым

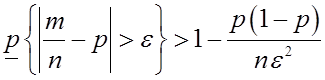
Вероятность  того, что разность между частостью и вероятностью события будет меньше , зависит от вероятности этого события  и числа проводимых испытаний.

а) Если , то вероятность того, что 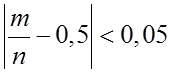 может быть определена из граничного условия

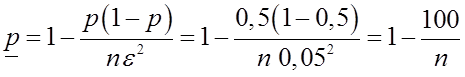
т.е. для того, чтобы

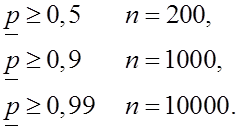
б) Если , то

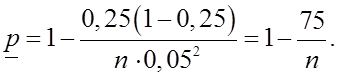
для

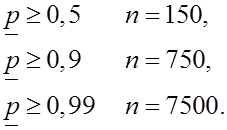
в) Если , а

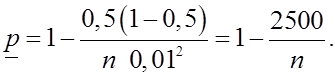
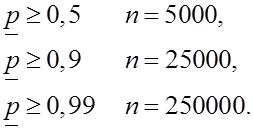
т.е. повышение требований к точности и надежности испытаний существенно увеличивает необходимый объем испытаний.

Теорема Бернулли с дополнением Чебышева легла в основу количественных критериев согласия, позволяющих проверить достоверность предлагаемой гипотезы по небольшому объему опытных данных.

ЗАДАЧА 1.2

Обработка результатов испытаний

с оценкой по среднеквадратичной погрешности

1) 

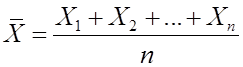
2)  - остаточные погрешности.

3)  Случайная погрешность  - разность между полученным из опыта значением и действительным значением, при условии, что все систематические погрешности исключены.

4)  При большом числе измерений законы для случайных и остаточных погрешностей совпадают.

5) 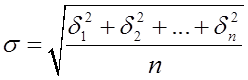  - средняя квадратичная погрешность ряда измерений.

6)  В этом случае - число погрешностей.

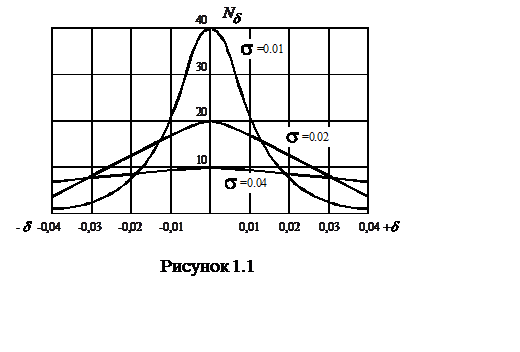
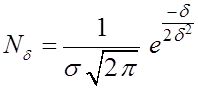
Если совокупность остаточных погрешностей не удовлетворяет нормальному распределению, то в ряде измерений есть систематические погрешности.

7) 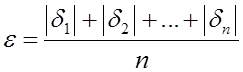  - средняя арифметическая погрешность.

8) 

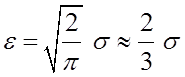
9) 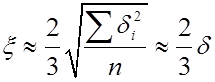  - вероятная погрешность.

10)  Формула Бесселя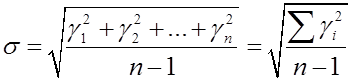

тогда

11) 

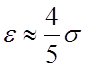
12) 

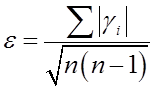
Если при обработке результатов испытаний значения  по 11 и 12 разнятся значительно, то, вероятно, есть систематическая погрешность.

13) 

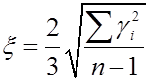
Исходя из 6 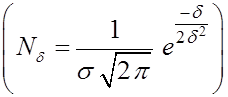 можно вычислить число измерений , необходимое для того, чтобы в ряду измерений только одна погрешность была бы больше заданной величины .

Вывод:

1) в 1 из 370 погрешность превысит , в 1 из 15635 погрешность превысит .

2) В практических измерениях появление погрешности больше, чем  почти исключено.

3) Появление погрешности большей чем  содержит промах и должно быть отброшено.

В итоге результат оценивается средним арифметическим. Точность результата характеризуется

 - средняя квадратичная

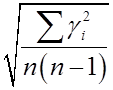
 - средняя арифметическая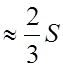

 - вероятная погрешность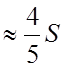

Пример. 16 раз замерялось сопротивление

Таблица 1.1

85,30	0,00	0,0000	85,30	+0,09	0,0081
85,71	+0,41	0,1681	85,71	+0,50	0,2500
84,94	-0,36	0,1296	84,94	-0,27	0,7290
84,70	-0,60	0,3600	84,70	-0,51	0,2601
85,63	+0,33	0,1089	85,63	+0,42	0,1764
86,65	+1,35	1,8225	-	-	-
85,24	-0,06	0,0036	85,24	+0,03	0,0009
85,36	+0,06	0,0036	85,36	+0,15	0,0225
84,86	-0,44	0,1936	84,86	-0,35	0,1225
85,21	-0,09	0,0081	85,21	0,00	0,0000
84,97	-0,33	0,1089	84,97	-0,24	0,0576
85,19	-0,11	0,0121	85,19	-0,02	0,0004
85,35	+0,05	0,0025	85,35	+0,14	0,0196
85,21	-0,09	0,0081	85,21	0,00	0,0000
85,16	-0,14	0,0196	85,16	-0,05	0,0025
85,32	+0,02	0,0004	85,32	+0,11	0,0121
Поэтому №6 отбрасываем и получаем правую часть			Нет . Окончательно .

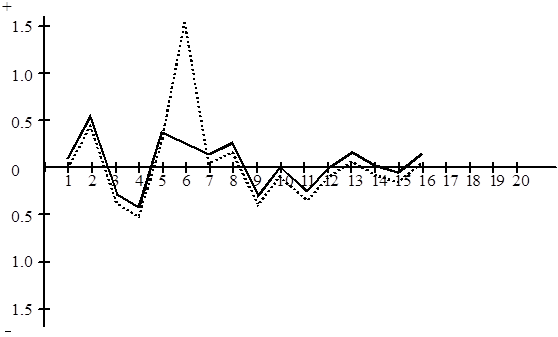Рисунок 1.2

Примечание: в принципе подобная процедура может повторяться до тех пор, пока погрешность измерения не будет считаться случайной, но обычно это наблюдается уже после первого цикла обработки.

ЗАДАЧА 1.3

Использование однофакторного дисперсионного анализа для проверки гипотез

Если какая-либо случайная величина  наблюдалась в  группах, то среднее значение ее в i-й группе

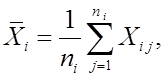
во всех группах

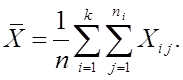
Полное рассеяние

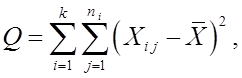
рассеяние между группами

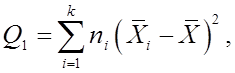
Остаточное рассеяние

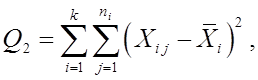
Примечание: .

Эти соотношения могут быть использованы для проверки однородности результатов в группах, т.е. возможности использования результатов для совместной обработки. Для этого сопоставляются две гипотезы:

1.  Основная – различие в результатах объясняется только случайностью.

2.  Противоположная - различие в результатах связано с наличием какого-либо определенного фактора.

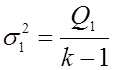 - эта случайная величина имеет распределение хи-квадрат с  степенями свободы.

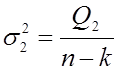 - эта случайная величина имеет распределение хи-квадрат с  степенями свободы.

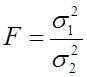 имеет  - распределение, поэтому полученное из опытов значение  сравнивается с теоретическим значением . Если , то принимается основная гипотеза, если  - противоположная.

Таблица 1.2

Квантили  95% вероятности

	1	2	3	4	5
1	161,4	199,5	215,7	224,9	230,0
2	18,5	19,0	19,2	19,2	19,3
3	10,1	9,6	9,3	9,1	9,0
4	7,7	6,9	6,6	6,4	6,2
5	6,6	5,8	5,4	5,2	5,0
6	6,0	5,1	4,8	4,5	4,4
7	5,6	4,7	4,3	4,1	4,0
8	5,3	4,4	4,1	3,8	3,7
9	5,1	4,2	3,9	3,6	3,5
10	5,0	4,1	3,7	3,5	3,3

Задача. По ( i ) 3 группам было проведено ( j ) 5 проверок, которые выявили различное