Линейное программирование (Составление плана использования технологических способов в производстве)

Министерство образования Российской Федерации

Санкт-Петербургский колледж Морского Приборостроения

Курсовая работа

По предмету: «Математические методы»

Тема: «Линейное программирование»

Специальность 2203, группа М-343

Выполнил студент:

Проверил преподаватель:

Оценка__________

Подпись_________

2006

Содержание:

1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ_ 3

1.1 Постановка задачи_ 3

1.2 Решение симплекс-методом_ 3

2 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ Л.П. 5

3.1 Нахождение начального плана транспортной задачи_ 13

3.1.1  Метод Северо-Западного угла 13

3.2. Нахождение оптимального плана методом потенциалов 13

4 ЗАКЛЮЧЕНИЕ_ 18

1 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

         1.1 Постановка задачи

На предприятии в процессе производства используются три технологических способа. При этом расходуются сырьё, трудовые ресурсы и учитываются накладные расходы. Известны удельные затраты aij каждого ресурса , запасы ресурсов bj ,(а также удельная прибыль сj) и удельное потребление воды dij при использовании каждого технологического способа.

Условия производства требуют, чтобы трудовые ресурсы были использованы полностью, а  накладные расходы были бы не меньше bj

Вид ресурсов	Технологические способы			Запасы ресурсов
	1(XI)	2(X2)	3(X3)
Сырьё(a1j)	3	2	1	26
Трудовые ресурсы (a2j)	1	1	2	11
Накладные расходы (a3j)	7	9	5	32
Расход воды (dij)	2	4	1

Требуется  составить план  использования технологических способов в производстве, обеспечивающий минимальное потребление воды.

При решении задач такого вида возникают следующие этапы:

1.- идентификация переменных

XI – 1-й технологический способ;

Х2 – 2-й технологический способ;

X3 – 3-й технологический способ;

2.  - определение целевой функции Функция минимального потребления воды:

f (х)= 2x1+4x2+1х3  min

3- Определение ограничений задачи

1)Сырьё:

3x1+2x2+1х3 26

2)Трудовые ресурсы:

1x1+1x2 +2 х3=11

3) Накладные расходы:

7x1+9x2+5х332

Математическая модель:

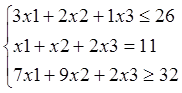
Линейный характер модели состоит в том, что и целевая функция и ограничения носят линейный характер, т.е. переменные в первой степени.

1.2 Решение симплекс-методом

В данной задаче ограничения являются равными по смыслу равенствами, следовательно в этом случаи прибегают к одноэтапному симплекс-методу.

В строке целевой функции выбирается максимально положительный коэффициент. Это будет соответствовать ведущему столбцу.

Составляется отношение элементов столбца ХО к соответствующим элементам ведущего столбца, кроме нулевых и отрицательных элементов, получившееся отношение записывается в столбец Отношение.

Из получившихся отношений выбирают минимальную величину. Это будет соответствовать ведущей строке. В случаи равенства выбирается любая.

На пересечении ведущей строки и ведущего столбца стоит ведущий элемент.

Ведущая строка соответствует переменной, которая выйдет из базиса, а ведущий столбец соответствует переменной, которая войдёт в базис.

Далее производится пересчёт всей таблицы:

1.      сначала пересчитывается  новая  ведущая  строка,  т.е. та,  которая вошла в базис(х2). Для этого надо старую ведущую строку разделить на ведущий элемент.

2.      все остальные строки пересчитываются одинаково:

Новая строка = Старая строка -  Новая ведущая строка* (коэффициент в ведущем столбце). Целевая функция может быть пересчитана методом коэффициентов.

Начальная таблица:

Базис	Х0	Х1	Х2	X3	S1	Z2	S3	Z3
S1	26	3	2	1	1	0	0	0
Z2	11	1	1	2	0	1	0	0
Z3	32	7	9	5	0	0	-1	1
F	0	-2	-4	-1	0	0	0	0

Первая итерация:

Базис	Х0	Х1	Х2	X3	S1	Z2	S3	Z3	Отношение
S1	26	3	2	1	1	0	0	0	13
Z2	11	1	1	2	0	1	0	0	11
Z3	32	7	9	5	0	0	-1	1	3.556
F	0	-2	-4	-1	0	0	0	0

Вводим  : X2   Выводим: Z3

Вторая итерация: