Математика \ Математические методы

Линейное программирование (Составление плана использования технологических способов в производстве), страница 2

Базис	Х0	Х1	Х2	X3	S1	Z2	S3	Z3	Отношение
S1	18,89	1,444	0	-0,111	1	0	0,222	0	x
Z2	7,444	0,222	0	1,444	0	1	0,111	0	5,154
Х2	3,556	0,778	1	0,556	0	0	-0,111	1	6,4
F	14,22	1,11	0	1,22	0	0	-0,444	0,444
Вводим : X3 Выводим: A2

Третья итерация:

Базис	Х0	Х1	Х2	X3	S1	Z2	S3	Z3	Отношение
S1	19,46	1,462	0	0	1	0,077	0,231	-0,231	13,32
X3	5,154	0,154	0	1	0	0,692	0,077	-0,077	33,5
Х2	0,692	0,692	1	0	0	-0,385	-0,154	0,154	1
F	7,923	0,923	0	0	0	-0,846	-0,538	0,444
Вводим : X1 Выводим: X2

Конечная таблица (кол-во итераций 3 )

Базис	Х0	Х1	Х2	X3	S1	Z2	S3	Z3	Отношение
S1	18	0	-2,11	0	1	0,889	0,556	-0,556	0
X3	5	0	-0,222	1	0	0,778	0,111	-0,111	0
Х1	1	1	1,444	0	0	-0,556	-0,222	0,222	0
F	7	0	0,133	0	0	0,333	0,333	-0,333
Оптимальное значение Ц.Ф. = 7

Х1*=1

X2*=0

X3*=5

Ответ: план, обеспечивающий минимальное потребление воды равен 7.

Все расчёты проводили в Excel.

2 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ Л.П.

Если число переменных в задаче меньше или равно 2, то возможно её графическое решение на плоскости, а именно в координатной системе X1;X2.

f (х)=2x1-3x2=>min

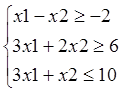
При графическом решении задачи отмечают следующие этапы:

1. - строят координатную плоскость X1;X2

- выбирают подходящий масштаб

- наносят на плоскость систему ограничений задачи, следующим образом:

a) сначала строят границу полученной плоскости в виде прямой

b) с помощью контрольной точки выбирают нужную полуплоскость

Таким образом строят все ограничения.

2. - выбирают общую для всех ограничений область, которая и будет областью допустимых решений (ОДР) задачи.

В данной задаче пятиугольник ABCDE. Каждая точка этой области является допустимым решением задачи. Нам нужно найти ту (те) точку (и) в которой функция принимает значение минимум . Для этого надо выполнить пункт 3.

3. - на чертеже строят два произвольных значения Z (целевой функции), для того чтобы определить направления её роста. Значения задают произвольно:

1 2 3 4 5 6 7 8

Скачать файл