Линейное программирование (Расчет питательности рациона скота, состоящего из комбикорма трех видов), страница 6

Нам нужно найти такую точку (точки), в которой целевая функция достигает своего max. Для этого построим в тех же координатах  два любых значения функции f(x) для того, чтобы узнать направление возрастания f(x).

Зададим произвольно:

Пусть f1(x)=12 и строим прямую f1(x)=12=4x1+3x2(3;0)(0;4)

f2(x)=0 пройдет через точку О(0,0)||f1

После построения двух значений целевой функции определяем направление ее роста, двигая прямую f(x) параллельно самой себе по ОДР в направление роста до крайней точки (отрезка) на  ОДР.

В точке B функция f достигает своего max.

Fmaxв точке B (XI *; Х2*)

Точка B образована пересечением II и VI ограничениями. Чтобы найти координаты этой точки решим совместно систему.

(.)В:    х1≤6                          х1=6

- 2x1+3x2≤42            -2·6+3х2=42        

3х2=54                    х1*=6

х2=18                    х2*=18

Подставим координаты точки B в выражение целевой функции.

Таким образом, найдено решение задачи.

fmax=4х1*+3х2*=4·6+3·18=24+54=78

Ответ: fmax=78

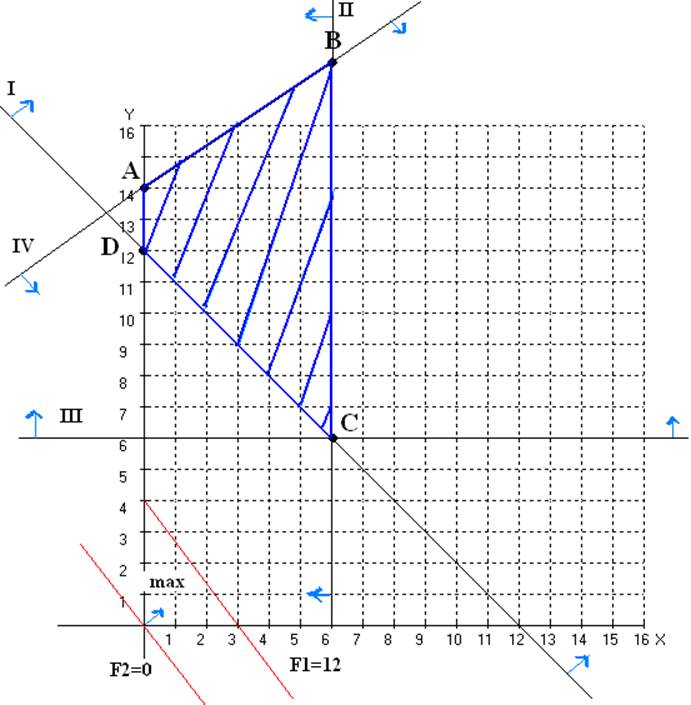
Рис.1.-Графический метод решения задачи

3 ТРАНСПОРТНАЯ ЗАДАЧА

3.1 Нахождение начального плана транспортной задачи

3.2 Метод Северо-Западного угла

Данная задача не сбалансирована, и для того чтобы её сбалансировать, в таблицу добавляется лишний столбец.

1) Начинаем с рассмотрения клетки х11=min{a1,b1}, возможны три варианта:

•   a1<b1, тогда  x11=a1 - первая строка выходит из рассмотрения, а новая величина b1'=b1- a1.

•   b1<а1=>х11=b1 - первый столбец выходит из рассмотрения.

a1'=a1- b1

•    a1=b1=>x11=al=b1 - первая строка и первый столбец выходят из рассмотрения и в дальнейшем будем иметь вырожденное решение

2)  Выбирают следующую Северо-Западную клетку и повторяют первый шаг и т.д..

3)  Последняя клетка заполняется автоматически.

4)  Считаем количество заполненных клеток в таблице, их должно быть (m+n-1) и план будет невырожденный. Если количество заполненных клеток оказалось меньше, чем (m+n-1), то план вырожденный и необходимо в этом случае дополнить недостающее количество, чтобы получилось (m+n-1). Для этого в клетку ставят 0, считая эту клетку заполненной.

Внимание:         При   постановке   0   не   должно   получаться   замкнутых прямоугольников.

5) Считается план

120    150      130      70

7	5	3	4
9	6	5	8
M	4	7	10