Физические процессы в электроприводе с машинами переменного тока, страница 4

Прежде чем записать формульные выражения для М_к и s_k, а также количественную зависимость M = f(s), получим простое и очень важное энергетическое соотношение для асинхронного двигателя.

Поскольку поле в воздушном зазоре вращается со скоростью w₀ , а электромагнитный момент имеет некоторое значение М, то электромагнитная мощность при этом выразится как

                                                       (4.12)

Мощность, потребляемая из сети (Р₁), если принять самое грубое приближение
(см. рис. 4.2, а), будет равна электромагнитной; если учесть R_s0 и X_ss0, она будет несколько больше, но часто все равно можно полагать, что  P₁P_эм           . Мощность на валу, очевидно, при этом будет равна: P₂ = Mw .

Теперь нетрудно обнаружить, что потери в роторной цепи (DР₂) составят:

.                                (4.13)

Последнее соотношение очень важно, поскольку позволяет при неизменной частоте  (f_s) и, следовательно, w₀  непосредственно оценивать энергетическую плату за отличие скорости ротора от синхронной, т.е. за регулирование скорости.

Формулы для механической характеристики

Выражение для DР₂ удобно при получении формул для M = f(s), M_Kи s_к. Действительно, приравняв потери DР₂ из формулы (4.13) их очевидному выражению  , получим:

.

Затем, подставив I'_r из формулы (4.9) и найдя экстремум функции M = f(s) и соответствующие ему М_к и s_к, получим уравнение механической характеристики, которое получило название уточненной формулы Клосса:

                                        ,                                         (4.14)

где а = R_s / R'_r; 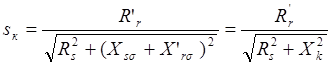  – критическое скольжение;
 - индуктивное сопротивление короткого замыкания.

Критический момент при этом выразится как

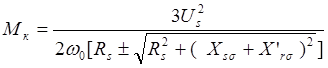,                             (4.15)

где знак «+» относится к двигательному режиму, а «-» – к генераторному.

Часто на практике полагают, что а = 0 если , т.е. пренебрегают активным сопротивлением обмотки статора (). Это обычно не приводит к существенным погрешностям при Р_ном > 5 кВт /4/, однако может неоправданно ухудшить модель при малых мощностях. При а = 0 выражения (4.14) – (4.16) становятся более простыми:

;                                                   (4.17)

;                                                                                             (4.18)

.                                                                                                                                                 (4.19)

Выражения (4.17) – (4.19) получили название упрощенных формул Клосса.

4.3. Параметры и режимы асинхронного электропривода

Номинальные данные машины

Выражения (4.14) – (4.19), полученные при принятых ранее допущениях, вместе с выражениями (4.2), (4.9), (4.13) очень полезны, так как они дают ответы на многие практические вопросы, в частности: какие величины и как влияют на вид механической характеристики, как можно регулировать скорость, момент или ток.

Прежде чем детально рассматривать сначала теоретические, а затем и практические аспекты асинхронного электропривода как системы, сопоставим найденное упрощенное математическое описание двигателя с номинальными данными, оценим допустимые границы изменения координат при регулировании.

Для асинхронного двигателя обычно известны номинальные напряжение (U_sном = U_ном,) частота (f_sном = f_1ном), ток (I_sном), выходная мощность (мощность на валу) (Р_ном), частота вращения (n_ном), КПД (h_ном), cosf_ном. Поскольку обмотка статора может быть соединена как в звезду, так и в треугольник, даются два значения линейных напряжения и тока: U_номY/U_номD и  I_sномY /I_{s номD}. Нетрудно обнаружить, что они соответствуют одним и тем же значениям фазных величин. Для короткозамкнутых двигателей указываются обычно кратности пускового тока (l_Iп = I_sп/I_{s ном})  и пускового момента (l_Mп = М_п / М_ном), а также кратность максимального момента (l_Mк = M_к / M_ном). В каталогах приводятся типовые естественные характеристики. Для двигателей с фазным ротором дополнительно указываются ЭДС на разомкнутых кольцах заторможенного ротора (Е_{r ном}) и номинальный ток ротора (I_{r ном}). В каталогах можно найти момент инерции двигателя, его массу.