Физические процессы в электроприводе с машинами переменного тока, страница 3

Действительно, при , т.е. при , обмотка ротора (примем ее для упрощения такой же, как на статоре) не пересекает силовых линий поля, и f_r = 0. При неподвижном роторе (w= 0,s = l) машина не отличается от обычного трансформатора, т.е. f_r = f_s.

Обнаружим, вместе с тем, что единственным источником, действующим в роторной цепи, является ЭДС (), наведенная по закону электромагнитной индукции в обмотке ротора (по-прежнему будем рассматривать одну фазу) и равная:

.                                                       (4.8)

Штрихами здесь и далее отмечены приведенные величины, учитывающие неодинаковость обмоток статора и ротора.

Учитывая, что обмотка ротора обладает сопротивлением () и индуктивностью рассеяния (), получим выражение для тока ротора ():

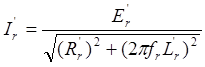
или после простых преобразований получим:

_,                                            (4.9)

где X΄_r – индуктивное сопротивление рассеяния фазы ротора при частоте питающего напряжения f_s.

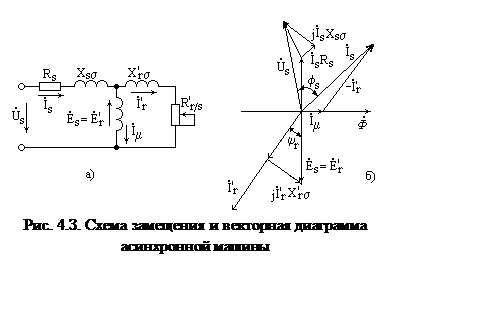
Нетрудно заметить, что мы пришли к обычной, самой распространенной схеме замещения фазы асинхронной машины (рис. 4.3, а). Схеме замещения соответствует векторная диаграмма (рис. 4.3, 6), наглядно представляющая связь между векторами всех величин в любом конкретном режиме.

Ограничения

Прежде чем использовать полученное представление для определения электромагнитного момента, характеристик и т.п., подчеркнем ограничения, соответствующие найденной модели.

Во-первых, она получена для одной фазы в предположении, что другие одинаковы и все напряжения симметричны. Нарушение любого из этих условий делает нашу модель неприменимой.

Во-вторых, модель отражает лишь временные соотношения и не содержит пространственных. Это справедливо при анализе установившихся процессов с периодическим изменением всех переменных, однако совершенно не отражает фактического положения в переходных режимах, когда существенный, а иногда и определяющий характер имеют свободные составляющие переменных. Поэтому и схема замещения, и векторная диаграмма пригодны только для анализа установившихся процессов.

В-третьих, модель неудобна, а чаще просто неприменима, если мы хотим в процессе управления двигателем формировать определенным образом за счет быстрых воздействий его токи и момент. В современных системах, так называемого векторного управления, мало иметь временные векторы, нужны и пространственные, т.е. другая модель.

Электромеханические и механические характеристики

Не задаваясь пока целью получения строгих формул, оценим главные черты любой механической характеристики, т.е. связи момента и скольжения (или скорости) с помощью универсального выражения для момента:

,                                     (4.10)

где k – некоторый конструктивный коэффициент;  – активная составляющая тока ротора;  – косинус угла между и .

Если мы проследим зависимость каждого из трех сомножителей в формуле (4.10) от скольжения (k примем постоянным), то получим представление и о произведении, т.е. об электромагнитном моменте машины.

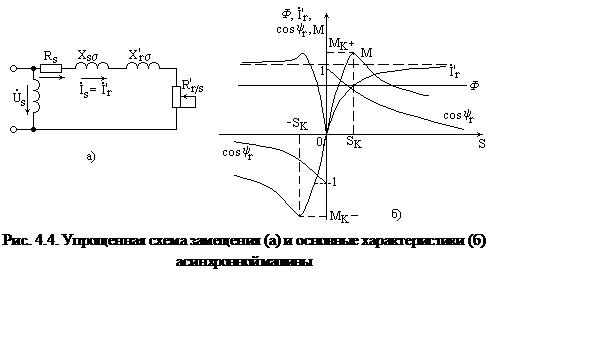
Магнитный поток (Ф) в первом приближении, как мы уже отмечали, не зависит от скольжения (рис. 4.4, б).

Ток ротора в соответствии с выражением (4.9) равен нулю при и асимптотически стремится к величине  при . Кивая  показана на рис. 4.4, 6.

Последний сомножитель  нетрудно определить из векторной диаграммы:

                        _.                                                               (4.11)

Он, очевидно, близок к  ±1 при малых s и асимптотически стремится к нулю при .

Теперь несложно представить качественно механическую характеристику
(рис. 4.4, б): момент равен нулю при s = 0 (w = w₀ ), достигает положительного (М_к+) и отрицательного (М_к-) максимумов или, как принято говорить, критических значений при некоторых значениях скольжения  ± s_k, также называемых критическими, а затем при стремится к нулю за счет третьего сомножителя.

Энергетические соотношения