Общественное потребление. Методы определения потребностей населения (Часть учебного пособия "Экономическая кибернетика"), страница 3

В практике анализа рядов экономической динамики широкое применение получили стохастические модели авторегрессии и скользящего среднего первого и второго порядков, которые могут быть получены как частные случаи уравнения (4.32).

Общие методы идентификации нестационарных рядов разработаны только для рядов, порожденных процессами со стационарными приращениями ц. С известным приближением этот тип процессов можно отнести к большинству рядов экономической динамики.

Если процесс содержит, например, липецкую тенденцию, то первые разности порождаемого им ряда стационарны. При логарифмической форме представления данных взятие первых разностей равносильно исключению экспоненциальной тенденции. Для циклического ряда периода Г первые разности ординат, взятые с интервалом Г, также стационарны и т. д. Критерием выбора порядка разностей, которые могут быть приняты как стационарная последовательность, является автокорреляция остатков.

Синтез динамической модели идентификации ряда со стационарными приращениями осуществляется посредством следующей процедуры:

1) берутся разности ординат </(т) наблюденного ряда столько раз (<у), чтобы получить стационарный остаток у (т.); .

2) подбирается стационарная модель с входным белым шумом, выход У (т), который идентифицирует полученный из (4.33) ряд у(х);

3) путем 5-кратного суммирования ряда У(т) вычисляется последовательность

(S  оператор суммирования), которая идентифицирует исходный ряд у(х}. А О Практически при идентификации нестационарного экономического ряда бывает достаточно формирование его разностей не выше второго порядка.

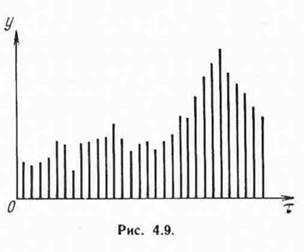
Для идентификации разнообразных экономических рядов, содержащих регулярную тенденцию, удобны конечно-разностные модели с правой частью, содержащей постоянный параметр 0^е. Такова, например простая модель

для которой выборочный ряд </(т) показан на рис. 4.9.

Для идентификации временных рядов, порождаемых процессами расширенного воспроизводства, можно также прибегнуть к модели (4.32). среди корней характеристического уравнения которой имеются |?.<,|>1.

В качестве примера рассмотрим временной ряд индексов национального дохода у (т) за 14 лет (для нулевого базового года индекс 100):

Модель его идентификации может быть построена в виде стохастического конечно-разностного уравнения (авторегрессии) первого порядка:  

для которого корень |Х|= 1,087. Поэтому она преобразует входной белый шум в нестационарный выход, моделирующий процесс расширенного воспроизводства с темпом, равным 8,7 %.

В практике анализа временных рядов, содержащих нестационарные и периодн- п ческие составляющие, часто прибегают к аппроксимации рядов с помощью надлежащим образом выбранных функций. Эта процедура, называемая обычно выравниванием ряда, не сопряжена с выявлением высокочастотных флуктуации, обусловленных множеством ненаблюдаемых факторов, и дает аналитическое представление регулярных компонент удобное, в частности, для целей их прогнозирования.

Выбранная из тех или иных априорных соображений пробная модель подлежит статистическому оцениванию и диагностической проверке. Для стационарных стохастических моделей процедура оценивания осуществляется методом максимального правдоподобия, рассматриваемым в курсах математической статистики. Среди различных способов диагностики оцененной модели наиболее широкое практическое применение получил корреляционный анализ остатков (остаточных ошибок) е(т), вычисляемых для принятой стационарной модели по данным временного ряда.

Фундаментальной проблемой анализа является построение многофакторных моделей, т.е. выявление причинно-следственных

97

связей между показателями экономического процесса и статистическая оценка их параметров по данным одновременно наблюдаемых рядов этих показателей. Особенно важно изучить связь между входными и выходными показателями.

Двумерная регрессионная модель (парная регрессия), связывающая траектории показателей входа н выхода объекта, представленных выборочными рядами х (т) и (/(т), строится аналогично рассмотренной выше одномерной модели. Полагая, что значения х{х} контролируемы (неслучайны), независимы и отсутствуют ошибки измерения показателей, регрессию У на Х аппроксимируют уравнением