При анализе и проектировании системы чаще всего имеют дело с зависимостями между входами элемента и его выходами (а не состояниями, с которыми выходы связаны функционально). Это обусловливается тем, что конечной целью управления системой обычно является не приведение ее в заданное состояние, а достижение требуемого воздействия на внешнюю среду. Поэтому элемент в общем случае рассматривается как преобразователь входов в выходы:
Y=[R}X, (2.1)
где R—символическое обозначение совокупности преобразований каждого входа в каждый выход. Если интенсивности входов элемента однозначно определяют его выходы, то поведение элемента детерминировано, в противном случае оно носит стохастический характер.
Структура системы. Функционирование системы как единого целого обеспечивается связями между ее элементами. В технической системе эти связи формируются при ее проектировании, в биологической они возникают естественным путем в процессе зарождения и развития организма. В экономических системах связи могут организовываться в плановом порядке или
27
I, складываться стихийно под воздействием рыночного механизма. Состав элементов и способ их объединения определяют структуру системы. Формально ее чаще всего представляют в виде графа, вершины которого соответствуют элементам системы, а дуги— их связям.
Взаимодействия реальных объектов—элементов системы друг с другом и с внешней средой — столь же разнообразны, как и свойства объекта и среды. При анализе и проектировании системы принимают во внимание лишь те связи, которые существенно влияют на ее функционирование; остальными пренебрегают, а в случае необходимости систему защищают от их возмущающего влияния (помех). Используя понятия входов элемента (число которых конечно), предполагают, что они моделируют именно существенные связи (материально-вещественные и информационные) между объектами. Таким образом, понятие «система» является абстракцией не только свойств охватываемых ею реальных объектов, но и связей между ними.
Формирование конкретной системы над заданным множеством объектов сопряжено с реализацией определенного отношения между их свойствами, существенными для выполняемых ею функций.
Формирование связей между элементами при их объединении в конкретную систему также можно рассматривать как реализацию определенного отношения над их входами и выходами. Этим отношением над множеством элементов (переменных) и задается структура системы.
Обратимся к примеру, иллюстрирующему это положение. Для описания системы будем пользоваться двумя способами:
графическим (схемным) и аналитическим—системой уравнений. Таким образом, в нашем изложении схема трактуется как графическая модель системы. От схемного описания можно перейти к аналитическому При этом предполагается, что каждый из элементов выполняет преобразования, свойственные ему до его включения в систему.
Кратко опишем этапы такого описания применительно к системе S (рис. 2.2). Ее элементы qi, Цг и </з— линейные преобразователи; <р и f—преобразователи, реализующие соответственно функции ф и f, 2i и ^2—сумматоры.
Для каждого из этих элементов возьмем соответствующие ему уравнения связи между его входами и выходами. Объединенные таким образом уравнения составят систему уравнений для 5. В нашем случае (для простоты предположим, что элементы являются статическими преобразователями):
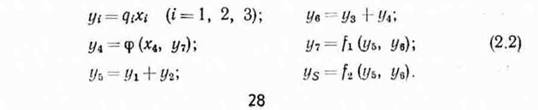
(2.2)
Число степеней свободы S системы определим как разность 2J, между общим числом переменных (л) и числом уравнений связей между ними (х). В нашем случае л=12, %=8, 2=4, т. е. система обладает четырьмя степенями свободы. При заданных четырех входах (^„ 1=1,4) состояние выхода детерминированной системы буде1 однозначно определено функцией ys=F(Xi, X2, Хз, х<,). Она может быть получена из уравнений (2.2) после соответствующих подстановок переменных. Представляется очевидным, что если система описана уравнениями (2.2), то нетрудно построить схему, показанную на рис. 2.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.