Горячая осадка цилиндрической заготовки с отверстием, страница 6

Метод баланса работ основан на законе сохранения энергии, согласно которому работа внешних сил на соответствующих перемещениях равна работе внутренних сил деформирования. При этом упругая деформация не учитывается, материал заготовки считается несжимаемым, а работа внутренних сил определяется через интенсивности деформаций сдвига и касательных напряжений. Данный метод может быть использован для определения деформирующих усилий при процессах осадки, ковки и объёмной горячей штамповки. Он не позволяет находить распределение полей напряжений и деформаций [11].                                                                                                              

3 Решение поставленных задач и обработка результатов

В нашем случае рассматриваем осадку заготовки верхней плитой. При таких внутреннем и внешнем диаметрах, и высоте заготовки происходит свободная осадка с  расширением полости заготовки.

                                                                           (37)     

Здесь и далее будут использованы относительные величины удельной силы, мощностей деформации и на­пряжений, отнесенные к средней ве­личине напряжения σ_sтекучести ма­териала заготовки (натуральное зна­чение удельной силы  ; µ — коэффициент трения по напряжению текучести, соответствующий закону контактного трения Зибеля , где β — коэффициент Лоде, среднее значение которого равно 1,1.

Формула для расчета удельной силы свободной осадки полой заготовки имеет вид:

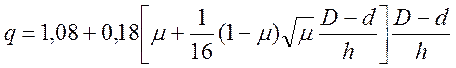                                           (38)

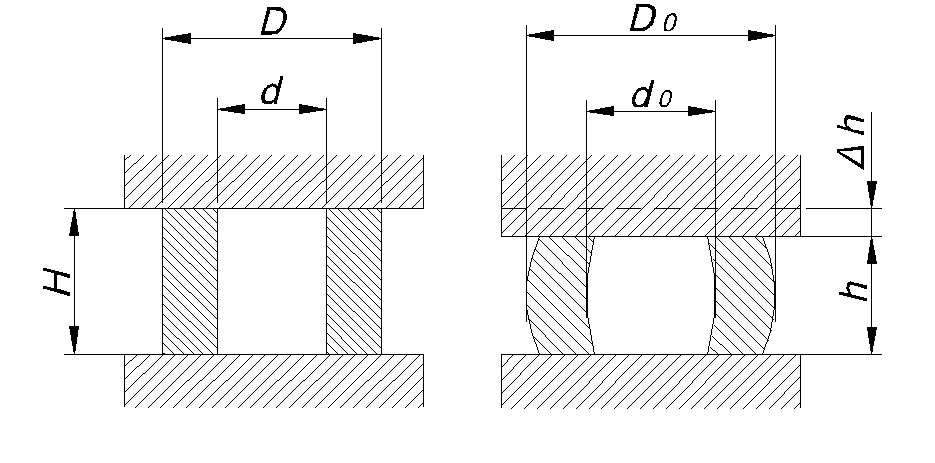
     Рис. 9. Схема осадки цилиндрической заготовки с внутренним отверстием.

Для горячей осадки стали исходя из характера нагрева, а также применяемой смазки принимаем следующее значение относительного контактного трения μ = 0,3.

Из этого следует

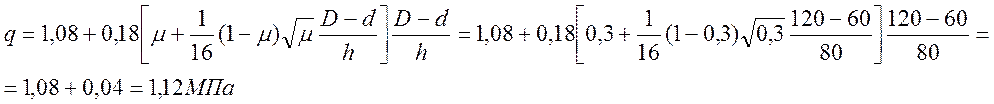
 Величина предела текучести деформируемого металла σ_S зависит от температурно – скоростных условий процесса деформации и может быть определена по формуле

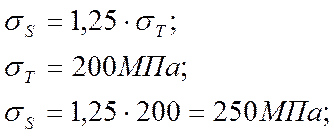                                                                (39)

   Натуральное зна­чение удельной силы будет равно:

    Сопротивление деформации металла будет создавать контактное трение.

                                                            (40)

Удельное усилие:

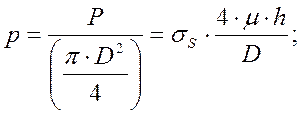                                                                           (41)                  

Подставляя значения в формулы (40) и (41) получаем

       

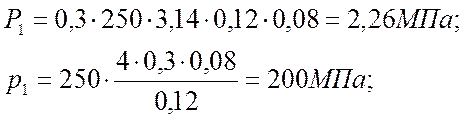
Для нахождения диаметра осаженной заготовки выберем осевую скорость пластического течения в виде

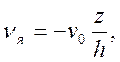                                         (42)

удовлетворяющем имеющимся граничным условиям: vz = -v0при z = h иvz = 0 при z = 0.

Из условия несжимаемости можно получить выражение радиальной скорости в виде

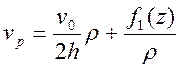                                     (43)

где  f1(z)— произвольная функция от координаты z

В случае идеальной осадки (т, е. осадки при μ = 0) vρ = 0 при р = 0. В нашем случае примем, что  vρ = 0 при p = Rv, где радиус Rv является искомой варьируемой величиной. С учетом этого условия из выражения (43) вытекает

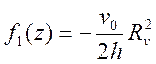 и

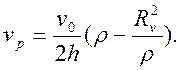                                   (44)

Подставляя выражения (41) и (44) в известные кинематические соотношения, находим скорости деформаций:

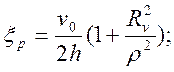
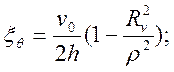
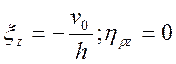
и интенсивность скоростей деформации

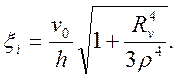                                      (45)

Для определения мощности внутренних сил в объеме V по выражению 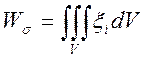применим теорему о среднем значении интеграла в виде 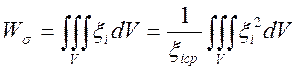, где примем, что .

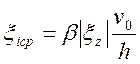Тогда с учетом выражения (45) мощность внутренних сил

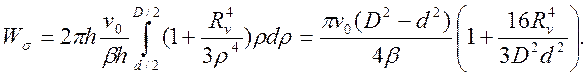             (46)

С учетом поверхности контакта с верхней и нижней плитами мощность сил контактного трения 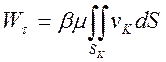в соответствии с выражением (44) будет

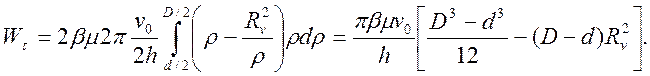          (45)

Сложив выражения (44) и (45), найдем полную мощность деформации:

        

Из условия минимума этой мощности δWq/δRv = 0 получаем уравнение

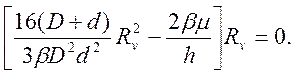                              (46)

         Уравнение (46) имеет два возможных решения. Решение Rv = 0 соответствует идеальной осадке и нас не интересует. Поэтому, приравнивая нулю выражение в квадратных скобках, находим:

           

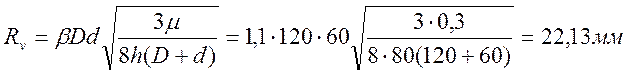
Полученное решение является общим, поскольку описывает и случай идеальной осадки:  Rv= 0 при μ = 0.

Далее, с целью упрощения расчета изменения диаметров в процессе осадки, будем считать, что радиус Rv определяется параметрами исходной заготовки и в процессе осадки не меняется:

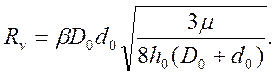                               (47)

С учетом выражения (45) напишем дифференциальное уравнение

                      

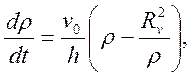
которое с учетом того, что

приводится к виду:

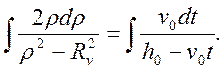
Отсюда получаем:

                                  (48)  

Произвольную постоянную С находим из начального условия ρ=ρ0 при t = 0:

                                      (49)

Подставив в равенство (48) выражения (47) и (49), получим:

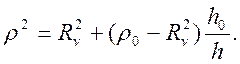                                  (50)

Для определения изменения внутреннего диаметра в процессе осадки подставим в формулу (15) ρ=d/2 и ρ0=d0/2. Кроме того, для удобства заменим Rv на Dv/2, в результате чего получим:

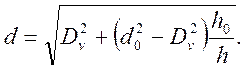                                  (51)

Подставив в формулу (11) β=1,1 и удвоив результат, окончательно найдем:

        (52)

Подставляя выражение (52) в выражение (51) получаем

        

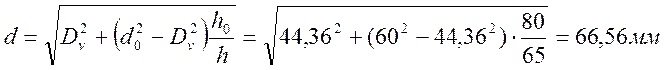
Если при расчете получим Dv > d0(что означает сужение, а не расширение полости), то в соответствии с физическим смыслом решаемой задачи следует принять Dv = d0.

Из условия постоянства объема следует:

               

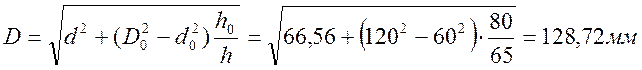
Степень деформации (%) при осадке:

                                     

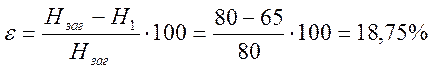
Касательное напряжение на предел текучести:

                                                                           (53)

Деформации при осадке:

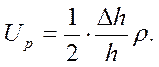
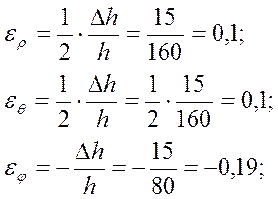
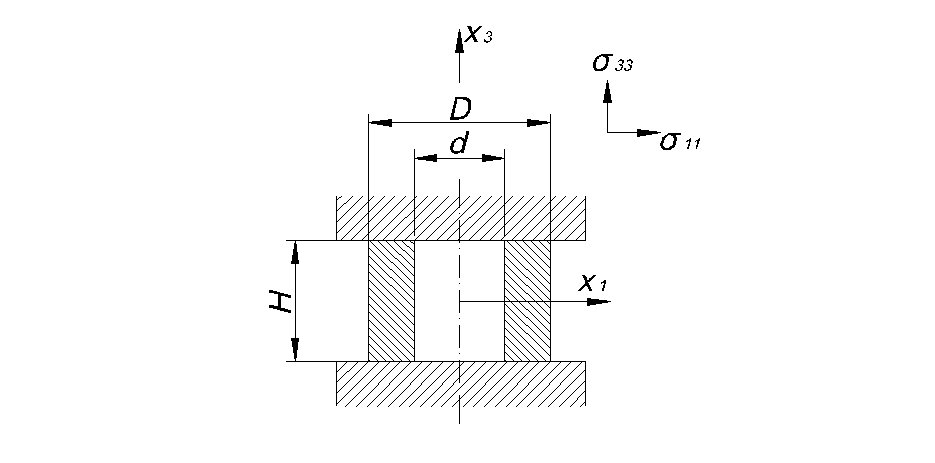
Рис. 10. Схема плоского напряжённого состояния

Для определения напряжений воспользуемся схемой плоской деформации.

                                                                    (54)

С учётом формулы (55) уравнения равновесия примут вид

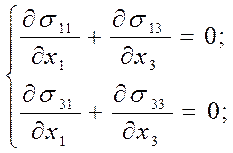                                                                            (55)