Если при расчете получим Dv > d0(что означает сужение, а не расширение полости), то в соответствии с физическим смыслом решаемой задачи следует принять Dv = d0.
Из условия постоянства объема следует:
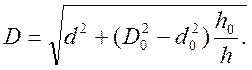 (18)
(18)
Выражения (16)—(18) позволяют определить изменение диаметров заготовки в процессе осадки с расширением полости.
Теперь
проанализируем случай свободной осадки полой заготовки с сужением полости (рис.
5). При такой осадке радиальное течение металла будет двусторонним, а искомым
варьируемым параметром является диаметр DГграницы,
отделяющей область 1, в которой металл движется наружу, от области 2, в которой
металл движется внутрь. Очевидно, что при ![]() . Таким образом, в области 1
рассматриваемая задача соответствует решению, полученному в работе [4] для
осадки полой заготовки на оправке, а в области 2 — решению, полученному в
работе [3] для осадки полой заготовки в матрице.
. Таким образом, в области 1
рассматриваемая задача соответствует решению, полученному в работе [4] для
осадки полой заготовки на оправке, а в области 2 — решению, полученному в
работе [3] для осадки полой заготовки в матрице.
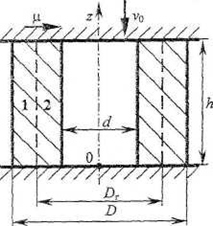
Рис. 5 Расчетная схема свободной осадки полой заготовки с сужением полости
Используя результаты данных решений, можно получить, что относительная удельная сила, действующая на область 1,
определяется выражением
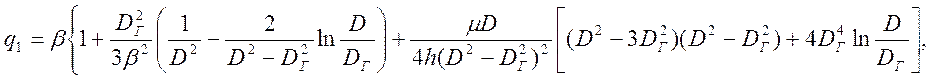 (19)
(19)
а относительная удельная сила, действующая на область 2, определяется выражением
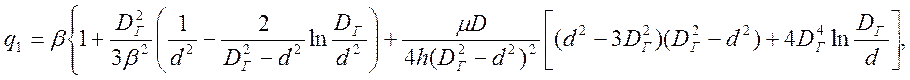 (20)
(20)
В выражениях (19), (20) следует принимать β = 1,1 при d/D ≥ 0,5 и β = 1 + 0,2d/D при d/D < 0,5. Последнее равенство учитывает то, что при уменьшении диаметра d отверстия площадь границы с плоским деформированным состоянием, определяемая диаметром DГ, будет уменьшаться, и при d = 0 задача перейдет в осадку сплошной заготовки с,
β = 1.
Умножив q1 и q2на соответствующие им площади и отнеся сумму полученных выражений к общей площади поперечного сечения, получим относительную удельную силу свободной осадки полой заготовки с сужением полости:
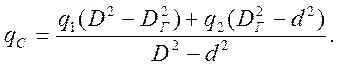 (21)
(21)
Искомый диаметр границы определяется из условия минимума:
![]() (22)
(22)
Поскольку уравнение (22) является трансцендентным, то его решение выполняется численным методом.
Значение Dr позволяет не только вычислить удельную силу свободной осадки с сужением полости, но и определить изменение средних диаметров заготовки.
Поскольку в процессе осадки отклонения d/D и h/D будут меняться, то будет меняться и величина Dr изменяется незначительно, показатели, что с достаточной точностью можно считать, что диаметр D1 определяется параметрами d0/D0 и h0/D0 исходной заготовки и в процессе осадки не меняется. В этом случае из условия построения объема для области 1(см. рис. 5) получаем:
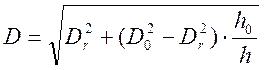 (23)
(23)
Из условия постоянства объема для области 2 находим:
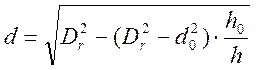 (24)
(24)
Использование для расчетов формоизменения формул (16)-(18) или (23,24) определяется сравнением qp и qc.
Если qp>qc, то будет происходить осадка с расширением полости, и расчеты следует вести по формулам (16-18). Если же qp<qc, то будет происходить осадка с сужением полости, и расчеты следует вести по формулам (23,24).
Удельную силу свободной осадки полых заготовок в любом случае целесообразно определять по наиболее простой формуле (3), что позволяет избежать использования более трудоемких формул (19)-(21), требующих нахождение Dr. Формула (3) строго соответствует случаю с расширением полости, а для осадки с сужением полости дает вполне приемлемую верхнюю оценку [7].
1.3 Основные характеристики и параметры процесса, получаемые расчетным путем
1.3.1 Определение удельных усилий осадки
Возьмем призму высотой h, имеющую в основании правильный многоугольник с числом сторон n и диаметром вписанной в основание окружности d. Плоскостями, проходящими через ось призмы и ее ребра, разделим объем призмы на n частей. В соответствии с принципом наименьшего сопротивления эти плоскости примем за плоскости раздела течения. Ось z совместим с осью призмы, а оси x и y направим, как показано на рис 6.
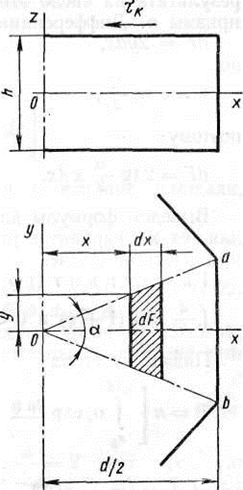
Рис. 6 Рассматриваемая призма
Так как все n частей, на которые разделена призма, одинаковы и оси x, y можно расположить, как показано на рис 6, в любой из этих частей, то рассмотрим распределение напряжений в одной такой части 0ab.
Предварительно сделаем одно допущение: примем, что в каждый данный момент при незначительной деформации форма поперечного сечения не изменяется и треугольник 0ab остается треугольником.
Отсюда вытекают такие следствия:
1) ![]() , а следовательно,
, а следовательно,
![]() .
.
2) в плоскостях, параллельных xy, касательные напряжения отсутствуют, т.е.
![]() , и имеются лишь
касательные напряжения
, и имеются лишь
касательные напряжения ![]() .
.
При этих условиях дифференциальные уравнения равновесия примут вид
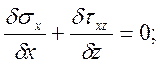 (а)
(а)
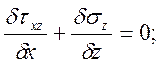 (б)
(б)
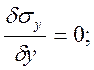 (в)
(в)
Из уравнения (в) явствует, что при сделанном допущении σy , а следовательно, и σx=σy не зависят от координаты y. Напряжение σz и τxz будем считать также независимыми от этой координаты.
Поскольку система дифференциальных уравнений (а) и (в) аналогична системе
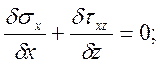
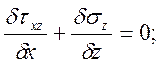 применяемой для плоской задачи, за
приближенное уравнение равновесия можно принять уравнение (25)
применяемой для плоской задачи, за
приближенное уравнение равновесия можно принять уравнение (25)
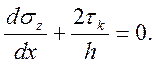 (25)
(25)
Решения его, выражающие напряжение σz в зависимости от координаты x,
будут теже самые, что и для плоской задачи, с той лишь разницей, что постоянную
![]() необходимо заменить на σs , а
размер a на
размер d.
необходимо заменить на σs , а
размер a на
размер d.
Для определения деформирующего усилия интегрирование будем проводить в зависимости от варианта равпределения напряжений по участкам площади треугольника 0ab с умножением результата на число этих треугольников, т.е. на число сторон призмы n. Дифференциал площади dF в этом случае рис 6
![]()
но
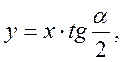
поэтому
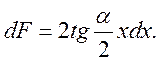
Выведем формулы для определения удельных усилий осадки для тех же вариантов распределения напряжений, которые были при плоской задаче.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.