Горячая осадка цилиндрической заготовки с отверстием, страница 2

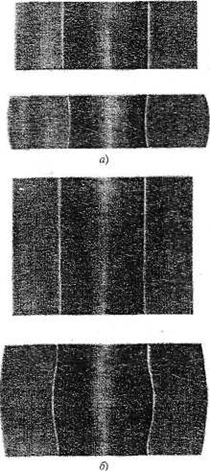
Рис. 3. Формоизменение при свободной осадке без смазки полых заготовок из стали Ст3 с варьированием высоты: а — при малой высоте (D0= 40 мм, d0 = 19 мм, h0 = 15 мм, D = 43 мм, d  = 17,5 мм, h = 12 мм); б — при большой высоте (D0=40 мм, d0 = 19 мм, h₀ =  30 мм. D = 44,5 мм, d= 20,5 мм, h= 25 мм)

do, мм	q	qy	qэ	σ, %
		МПа
50 40 24	1,424 1,629 2,004	3,560 4,074 5,009	4,0 5,0 6,2	12,3 22,7 23,8

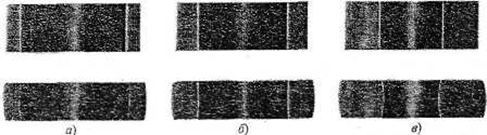
Рис. 4. Формоизменение при свободной осадке без смазки полых заготовок из стали Ст3 с варьированием внутреннего диаметра:

а – D0 = 40 мм, d0 = 32 мм, h0 = 15 мм, D = 42,3 мм, d= 32,5 мм, h = 12 мм; б – D0 = 40 мм, d₀ = 28 мм, h₀ = 15 мм, D = 42,5 мм, d = 28,0 мм, h = 12 мм; в – D0 = 40 мм, d0 = 19 мм, h₀=15 мм, D = 43,0 мм, d = 17,5 мм, h = 12 мм

В работе [10] ав­торы приводят значения, полученные по данной формуле, и собственные экспериментальные данные и утвер­ждают, что расчетная кривая очень близка к опытной. Однако наша проверка показала, что расчеты по формуле (2) не соответствуют изо­браженной теоретической кривой и сильно отличаются от эксперимен­тальных данных в сторону заниже­ния, что хорошо видно из таблицы, в которой приведены опытные q_э и вычисленные q_yпо формуле (2) значения удельной силы свободной осадки полой стальной заготовки на сухих шероховатых плитах при D0 = 70 мм, h0 = 6 мм, µ = 0,5, σs = 25 МПа. Кроме того, теоретическая кривая не соответствует формуле (2) не только количественно, но и качественно. Так, при  на графике в работе [1] q = 0, в то время как по формуле (2) q = 1,08.

Таким образом, улучшение теории свободной осадки полой заготовки является актуальным.

Сначала рассмотрим случай свободной осадки с расширением полости, расчетная схема которого представлена на рис. 1. В этой схеме применена цилиндрическая система координат ρ, θ, z  с началом координат на поверхности неподвижного инструмента. Осаживающий инструмент движется со скоростью v0. Материал считаем жесткопластическим, а упрочнение учитываем средней по очагу пластической деформации величиной напряжения σs текучести.

Выбрав кинематически возможное поле скоростей течения в виде выражений из работы [4] для осадки сплошной цилиндрической заготовки, можно показать, что в случае осадки полой заготовки формула нормальных напряжений на поверхности контакта с верхним инструментом имеет вид:

.

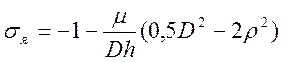С учетом этого относительная удельная сила свободной осадки с расширением полости

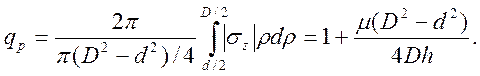     (3)

Может показаться, что определение диаметров заготовки после свободной осадки с расширением полости является несложной задачей, именно потому и не рассмотренной в работе [10]. Однако это не так. Несмотря на преимущественно малое трение и значительно большую равномерность деформации (см. рис. 2. а), чем при осадке с сужением полости (см. рис. 2, б), определение формоизменения при осадке с расширением также представляет собой вариационную задачу, результат которой зависит от коэффициента трения и соотношения размеров заготовки.

Кинематически (и практически, см. рис. 4, 6) возможно, что в рассматриваемом случае свободной осадки внутренний диаметр меняться не будет или будет увеличиваться на ту или другую величину, которую невозможно определить из чисто геометрических соображений. По условию постоянства объема соответствующее неопределенное приращение получит и наружный диаметр.

Для решения вариационной задачи выберем осевую скорость пластического течения в виде

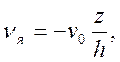                                  (4)

удовлетворяющем имеющимся граничным условиям: vz = -v0при z = h иvz = 0 при z = 0.

Тогда аналогично тому, как это сделано в работе [4], из условия несжимаемости можно получить выражение радиальной скорости в виде

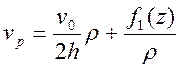                               (5)

где  f1(z)— произвольная функция от координаты z

В случае идеальной осадки (т, е. осадки при μ = 0) vρ = 0 при р = 0. В нашем случае примем, что  vρ = 0 при p = Rv, где радиус Rv (см. эпюру скорости vρ на рис. 1) является искомой варьируемой величиной. С учетом этого условия из выражения (5) вытекает

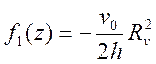                    и

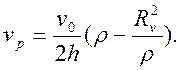                               (6)

Подставляя выражения (4) и (6) в известные кинематические соотношения, находим скорости деформаций:

                  

                  

                  

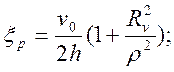
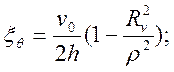
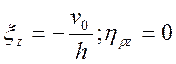
и интенсивность скоростей деформации

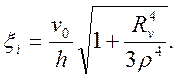                                   (7)

Для определения мощности внутренних сил в объеме V по выражению 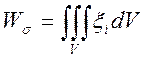применим теорему о среднем значении интеграла в виде 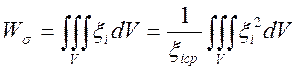               , где примем, что .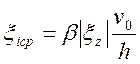

Тогда с учетом выражения (7) мощность внутренних сил

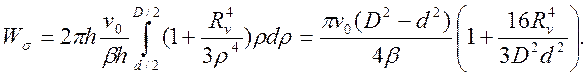           (8)

С учетом поверхности контакта с верхней и нижней плитами мощность сил контактного трения 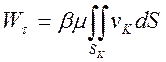в соответствии с выражением (6) будет

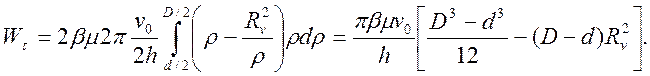        (9)

Сложив выражения (8) и (9), найдем полную мощность деформации:

      

Из условия минимума этой мощности δWq/δRv = 0 получаем уравнение

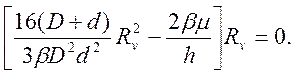                            (10)

         Уравнение (10) имеет два возможных решения. Решение Rv = 0 соответствует идеальной осадке и нас не интересует. Поэтому, приравнивая нулю выражение в квадратных скобках, находим:

               

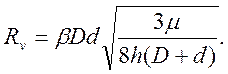
Полученное решение является общим, поскольку описывает и случай идеальной осадки:  Rv= 0 при μ = 0.

Далее, с целью упрощения расчета изменения диаметров в процессе осадки, будем считать, что радиус Rv определяется параметрами исходной заготовки и в процессе осадки не меняется:

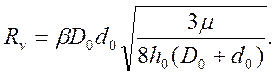                             (11)

С учетом выражения (6) напишем дифференциальное уравнение

                 

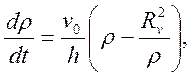
которое с учетом того, что

                     

приводится к виду:

                  

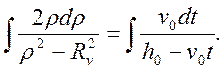
Отсюда получаем:

                                (13)  

Произвольную постоянную С находим из начального условия ρ=ρ0 при t = 0:

                                    (14)

Подставив в равенство (13) выражения (12) и (14), получим:

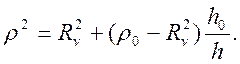                                (15)

Для определения изменения внутреннего диаметра в процессе осадки подставим в формулу (15) ρ=d/2 и ρ0=d0/2. Кроме того, для удобства заменим Rv на Dv/2, в результате чего получим:

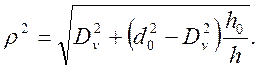                               (16)

Подставив в формулу (11) β=1,1 и удвоив результат, окончательно найдем:

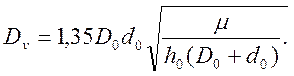                             (17)