Горячая осадка цилиндрической заготовки с отверстием, страница 4

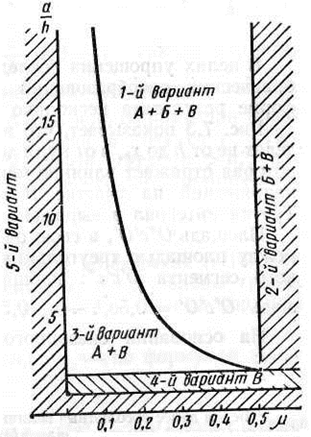
Рис 7 График распределения напряжений

1-й вариант (три участка )

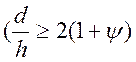 и  .

Пишем интеграл

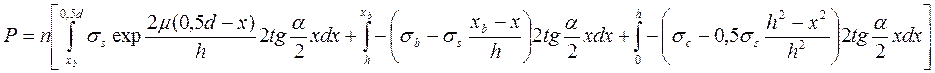
После интегрирования, подстановки значений σ_b и σ_c и деления на площадь контакта 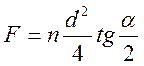  получим

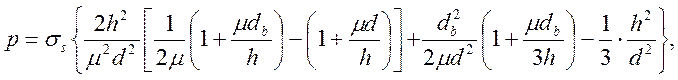             (26)

где

                                              

Последний член в фигурных скобках отражает влияние падения касательных напряжений на центральном участке.

2-й вариант (два участка – Б и В) 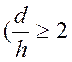 и

Деформирующее усилие для этого варианта

               

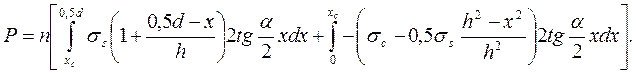
Произведя интегрирование и отнеся к еденице площади получим

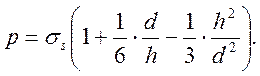                                                                           (27)

Эту формулу можно получить из предыдущей (26) путем подстановки в последнюю μ=0,5 и d_b=d.

Пренебрегая в формуле (27) последним членом в скобках, учитывающим влияние падения касательных напряжений на центральном участке, получим

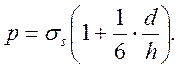                                                                                     (28)

Вычисление p по формуле (28) при 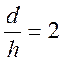 дает результат всего на 7,5% больший, чем по формуле (27), и составляет по абсолютной величине лишь 1/12σ_s . Таким образом, участок падения касательных напряжкеий здесь играет роль значительноменьшую, чем в формулах для осадки полосы в условиях плоской деформации, и практического значения не имеет.

Ранее была выведена (для цилиндра) методом баланса работ формула

                                              

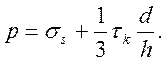
Если в этой формуле принять , как это сделано в рассматриваем варианте, то получим формулу (28). Таким образом, результаты обоих методов совпадают.

3-й вариант (два участка – А и В)  и

Деформирующее усилие

               

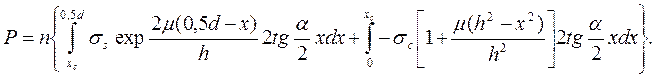
Интегрируя и деля на площадь контакта 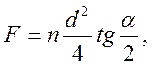 имеем

                        

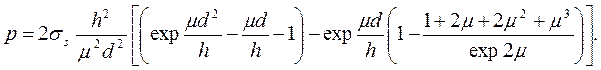
В этой формуле второй член в квадратных скобках отражает влияние падения касательных напряжений на центральном участке. Однако он имеет очень малое значение, и учитывать его нет практического смысла. Отбрасывая этот член, получим расчетную формулу для 3-го варианта

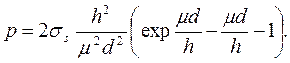                                                                (29)

4-й вариант (один участок В) 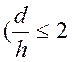 и .

Деформирующее усилие

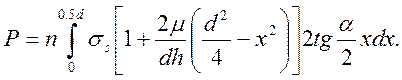
После интегрирования и деления на площадь основания 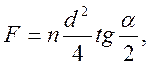 получим

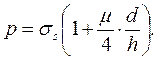                                                                                           (30)

5-й вариант

При μ=0 и любых значениях d/h, а также при , но при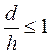

                                                                                                         (31)

Формулы (2-7) являются общими и для правильных призм, и для цилиндра, так как при неограниченном увеличении числа сторон правильного многоугольника, являющегося основанием призмы, последняя переходит в цилиндр.

Поскольку же поперечные сечения любой призмы в процессе ее осадки стремятся принять форму круга, постольку выведенные формулы следует считать пригодными и для промежуточных переходных форм поперечных сечений, образующихся в процессе осадки.

Формулы (26, 28, 29, 30) для случая осадки цилиндрической поковки вывел Е.П. Унксов. Он также провел обширные экспериментальные исследования, подтверждающие их правильность.

Формулы (26 и 29) достаточно сложны для вычислений. Поэтому следует рекомендовать пользоваться на практике графиками. График на рис 2 показывает, что интенсивность влияния роста коэффициента трения на удельное усилие уменьшается при увеличении его значений. Кривые для μ≥0,25 весьма близки к кривой для μ=0,5. Это дает возможность рассчитывать удельное усилие при горячей осадке, когда коэффициент трения большой, по приближенной формуле (4)

                                                  

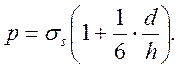
Для расчета удельного усилия при осадке с применением смазки можно воспользоваться ранее полученной формулой 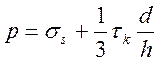 , положив в ней :

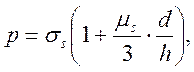                                                                                    (32)

где μ_s-фактор трения.

Эта формула широко известна под наименованием формулы Э. Зибеля.

Все приведенные выше формулы, пригодные для определения удельных усилий осадки правильной призмы и круглого цилиндра, можно получить на базе рассмотрения осадки цилиндра, используя условия равновесия в цилиндрических координатах.

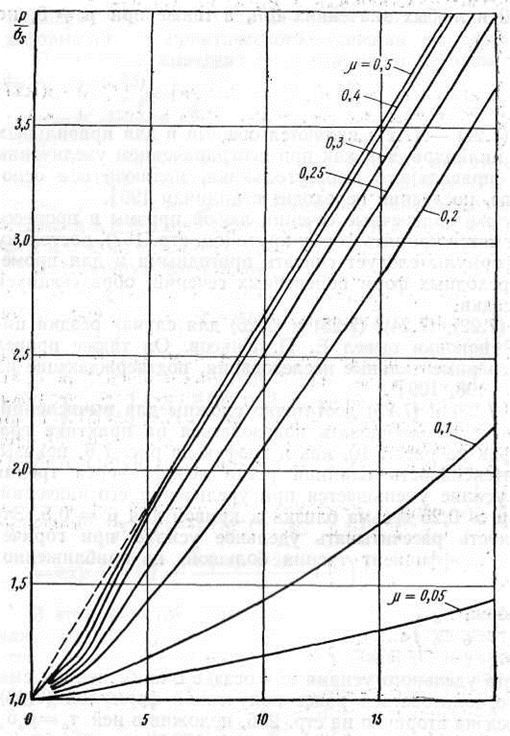
Рис. 8 График интенсивности влияния коэффициента трения на удельное усилие

Возьмем первое уравнение системы

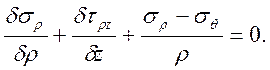
Учтем, что на контактной поверхности напряжения  и не зависят от координаты z и , поскольку .

Допустим также, что  является линейной функцией z. Тогда получим

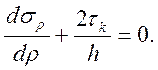
Приняв условие пластичности в форме 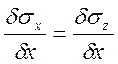 или , имеем

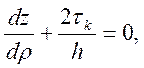
т.е. уравнение, аналогичное уравнению 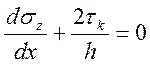, на основании которого были получены все формулы, относящиеся к осадке правильной призмы и круглого цилиндра [9].

1.3.2 Работа деформирования при осадке

Пусть в какой то момент процесса осадки при деформирующем усилии, равном P, высота тела уменьшается на бесконечно малую величину dh. Тогда элементарная работа деформирования

 dA=Pdh,

а полная работа деформирования при уменьшении высоты от начальной h0 ной h

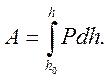
Поскольку имеет значение абсолютная величина работы, переставим пределы интегрирования

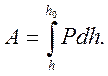
Но деформирующее усилие P=pF, где p – переменное удельное усилие деформирования, а F – также переменная площадь контакта. Следовательно

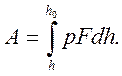                                                                                               (33)

Выражение (33) представляет собой наиболее общее выражение работы деформирования.

Если предположить, что площадь поперечных сечений осаживаемого тела в процессе осадки постоянны по высоте, т.е. бочкообразность отсутствует, то на основании условия постоянства обьема

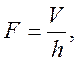
где V – постоянный объем осаживаемого тела. Подставляя в уравнение 9, имеем

 

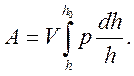
Так как p – величина переменная и зависит от h, то вынести p за знак интеграла нельзя. Однако, учитывая теорему о среднем значении, можно написать

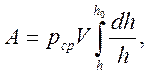
где pср – некоторое среднее значение удельного усилия в промежутке h0 – h.

Интегрируя, получим

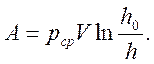
Произведение 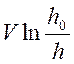 представляет собой абсолютную величину смещения объема Vc , и, следовательно,

.

Таким образом, работа деформирования равна произведению среднего усилия на смещенный объем.

В идеальном случае осадки без трения и упрочнения удельное давление равно напряжение текучести, и тогда

                                                                                                  (34)