Оценка распределений. Двухмерное и одномерное распределение

ЗАДАЧА II. ОЦЕНКА РАСПРЕДЕЛЕНИЙ

После графического анализа появляется необходимость получить вероятностные характеристики генеральной совокупности более точно. Для этого следует построить соответствующие вероятностные пространства.

Для изучения фонового массива применяется методика исследования больших выборок. Строятся одномерные распределения Х и Y каждой из компонент и совместно двухмерное распределение (Х,Y).

На аномальные участки А и В продемонстрирована методика исследования малых и очень малых выборок.

Цель задачи II. Для каждой выделенной в предварительном анализе генеральной совокупности построить  и оценить одномерные распределения Х и Y каждой из компонент и совместное распределение (Х,Y).

Перечислим по шагам этапы решения этой задачи.

Шаг 1. Двухмерное распределение:

·  анализ особых точек;

·  дискретизация множества исходов;

·  двухмерная гистограмма частот;

·  выбор ложных нулей;

·  двухмерная гистограмма относительных частот.

Шаг 2. Одномерные распределения компонент:

·  гистограммы и интегральные функции распределения больших выборок;

·  интегральные функции распределения малых выборок;

·  гистограммы малых выборок;

·  сравнительный анализ интегральных функций, сравнительный анализ гистограмм.

Для того, чтобы описать вероятностную картину поведения (х,у) строится двухмерное распределение вероятностей совместного распределения (X,Y).

Шаг 1. Двухмерное распределение

 «Фоновый» массив

Построим поле корреляции (синонимы – «диаграмма рассеяния», «облако наблюдений»), т.е. изобразим на координатной плоскости (х,у) исходные точки «фонового» массива наблюдений (x_i ,y_i) из табл. А.

При этом «подозрительные точки», отмеченные на протоколе (рис. I.2), отметим также и на корреляционном поле (рис.II.1), чтобы их не терять из виду.

1.1. Анализ особых точек

При анализе поля корреляции «фонового» массива С можно сделать следующий вывод: точки, которые были отмечены как особые (i=43; 69; 99; 51) не выделяются из основного облака и не нарушают общую зависимость и, следовательно, их поведение можно считать вполне регулярным, то есть данные точки особыми не являются.

Замечание: если точки являются особыми (резко выделяются из основного облака наблюдений, не отражают общую зависимость), то при дальнейшем анализе их значения не учитываются.

1.2. Дискретизация множества исходов

Облако наблюдений разбивается на равные интервалы длиной h_x по оси х и длиной h_y по оси y.

Замечание: в общем случае h_xh_y.

Число интервалов определяется по формуле Стержесса k=1+3,3lg(n) или, основываясь на теории, выбирается между ln(n) и , где n-объём выборки. Нужно помнить, что слишком крупная разбивка скрадывает нюансы и огрубляет последующие вычислительные оценки. Слишком дробная (мелкая) разбивка, напротив, чувствительна к случайным «причудам» выборки.

В нашем примере n=75, ln(n)=4.3, =8.7 – значит, годится 5-8 интервалов. Используя формулу Стержесса, окончательно получаем k=1+3,3lg(n)»7.

Замечание: количество интервалов по х и по у может быть не одинаковым (скажем, по х – 6 интервалов, а по у- 7 интервалов).

Таким образом «облако интервалов» разбито на прямоугольные клетки, которые являются исходами в дискретном двухмерном пространстве (рис. II.1).

Обозначим через  точки середины интервалов разбивки по х; аналогично  - точки середины интервалов по у. Точка (,), которая является центром прямоугольника разбиения, однозначно указывает исход.  называется j-й вариантой х, а  - k-й вариантой у.

Корреляционное поле: группировка наблюдений

Фоновый массив С

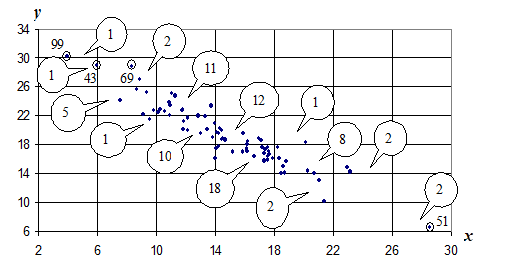Рис. II.1

1.3. Двухмерная гистограмма частот

После разбивки «облака наблюдений» на прямоугольные клетки – исходы, подсчитывается число точек в каждом прямоугольнике и записывается число прямо в нём.

Итого такой обработки «облака» переносятся в «группировочную таблицу» (табл. II.1).

Таблица II.1

h_x=4.0;С_х=16.0;h_y=4.0; С_у=20.0

	4.0	8.0	12.0	16.0	20.0	24.0	28.0	nk	vk
8.0							1	1	-3
12.0					2			2	-2
16.0				18	8	2		28	-1
20.0		1	10	12	1			24	0
24.0		5	11					16	1
28.0	1	2						3	2
32.0	1							1	3
nj	2	8	21	30	11	2	1	75=n
uj	-3	-2	-1	0	1	2	3