Оценка распределений. Двухмерное и одномерное распределение, страница 2

В таблице использованы следующие обозначения:

n_jk–число точек в прямоугольнике (,);

n_j,n_k – суммы n_jk  по столбцам и строкам;

n – объём выборки, равный сумме всех n_jk. .

1.4. Выбор ложных нулей

Следующий шаг – «выбор ложных нулей». Подробнее – прил.2.

Введём «условные» переменные (u,v), связанные с исходными переменными (x,y):

x=C_x+h_xu;           y=C_y+h_yv,

где h_x и h_y – длины интервалов группировки;

C_x и C_y –  «ложные нули».

Для «фонового» массива С  (см. табл. II.1) выбираем: C_x=16.0, C_y=20.0, h_x=h_y=4.0.

1.5. Двухмерная гистограмма относительных частот

Если каждое значение n_jk  таблицы II.1 поделить на общее количество точек (для «фонового» массива n=75), то получим распределение относительных частот w_jk=, которое является оценкой вероятности попадания (x,y) в прямоугольник (,) (табл. II.2).

Таблица II.2

h_x=4.0;h_y=4.0

	4.0	8.0	12.0	16.0	20.0	24.0	28.0	wk
8.0							0.013	0.013
12.0					0.027			0.027
16.0				0.240	0.107	0.027		0.374
20.0		0.013	0.133	0.160	0.013			0.319
24.0		0.067	0.147					0.214
28.0	0.013	0.027						0.040
32.0	0.013							0.013
wj	0.026	0.107	0.280	0.400	0.147	0.027	0.013	1

«Аномальные»серии А и В

Обрабатываем «аномальные» серии А и В аналогично «фоновому» массиву (рис. II.2, табл. II.3, табл. II.4).

Корреляционное поле: группировка наблюдений

Аномальные участки А и В

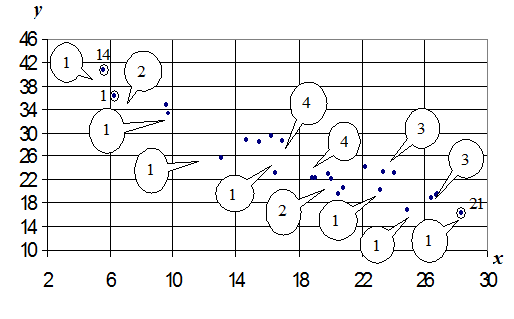
Рис. II.2

Таблица II.3

Двумерная гистограмма частот

«аномальные» серии А и В

h_x=4.0;С_х=16.0;h_y=4.0; С_у=28.0

	4.0	8.0	12.0	16.0	20.0	24.0	28.0	nk	vk
16.0						1	1	2	-3
20.0					2	1	3	6	-2
24.0			1	1	4	3		9	-1
28.0				4				4	0
32.0		1						1	1
36.0		2						2	2
40.0	1							1	3
nj	1	3	1	5	6	5	4	25=n
uj	-3	-2	-1	0	1	2	3

Таблица II.4

Двумерная гистограмма относительных частот

«аномальные» серии А и В

h_x=4.0;h_y=4.0