Величина ![]() рассчитывается с учетом
того, что пазы имеются как на поверхности статора, так и на поверхности ротора
рассчитывается с учетом
того, что пазы имеются как на поверхности статора, так и на поверхности ротора 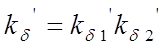 , где
, где 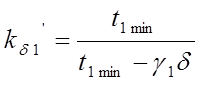 -коэффициент
Картера для статора;
-коэффициент
Картера для статора; 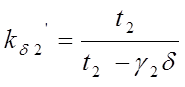 - коэффициент Картера для
ротора;
- коэффициент Картера для
ротора; 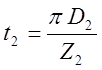 - зубцовый шаг ротора;
- зубцовый шаг ротора;
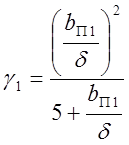 ,
, 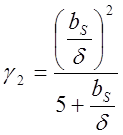 - коэффициенты, учитывающие открытие
пазов (рис. 19, 20).
- коэффициенты, учитывающие открытие
пазов (рис. 19, 20).
Проводимость лобового рассеяния обмотки статора
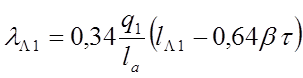 , где
, где ![]() -
средняя длина лобовых частей, приходящаяся на один полувиток катушки
(определяется по чертежу катушки);
-
средняя длина лобовых частей, приходящаяся на один полувиток катушки
(определяется по чертежу катушки); 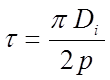 - полюсное
деление статора.
- полюсное
деление статора.
Реактивное сопротивление обмотки ротора для
синхронной частоты ![]() и учетом того, что
и учетом того, что ![]() представляется как
представляется как ![]() , где
, где ![]() ,
,![]()
![]() -
проводимости рассеяния соответственно пазовой и лобовой частей обмотки и по
коронкам зубцов.
-
проводимости рассеяния соответственно пазовой и лобовой частей обмотки и по
коронкам зубцов.
Проводимость пазового рассеяния обмотки
ротора при грушевидных пазах (рис. 20) 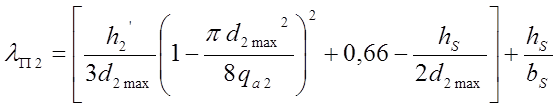 ,
где значения
,
где значения ![]() ,
, ![]() ,
,
Проводимость дифференциального рассеяния обмотки ротора
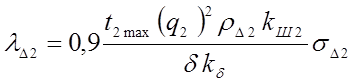 , где
, где 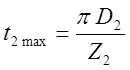 –
зубцовый шаг по внешнему диаметру ротора;
–
зубцовый шаг по внешнему диаметру ротора; 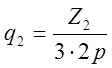 -
число витков на полюс и фазу ротора;
-
число витков на полюс и фазу ротора; ![]() ;
; 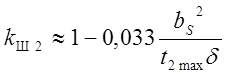 - коэффициент учета открытия паза;
- коэффициент учета открытия паза; ![]() - коэффициент дифференциального
рассеяния (рис. 23).
- коэффициент дифференциального
рассеяния (рис. 23).
Проводимость лобового рассеяния обмотки, если
кольца примыкают к стали ротора (при литой алюминиевой обмотке) 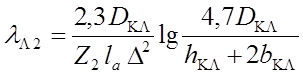 .
.
Расчет характеристик холостого хода и рабочих
характеристик АТД после конструктивной проработки
выполняется с использованием Т-образной схемы замещения (рис. 24). При
этом ротор рассматривается как неподвижный, а параметры его обмотки приводятся
к параметрам статорной обмотки ![]() - активное
сопротивление ротора, приведенное к параметрам статорной обмотки;
- активное
сопротивление ротора, приведенное к параметрам статорной обмотки; ![]() - реактивное сопротивление ротора,
приведенное к параметрам статорной обмотки , где
- реактивное сопротивление ротора,
приведенное к параметрам статорной обмотки , где 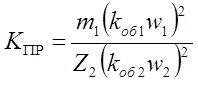 -
коэффициент приведения. Кроме того, механическая нагрузка двигателя заменяется
переменным активным сопротивлением
-
коэффициент приведения. Кроме того, механическая нагрузка двигателя заменяется
переменным активным сопротивлением 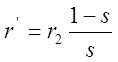 , позволяющим
учитывать все потери в двигателе (рис. 24). Энергетический баланс в двигателе
при такой схеме замещения может быть представлен векторной диаграммой (рис. 25)
и системой уравнений
, позволяющим
учитывать все потери в двигателе (рис. 24). Энергетический баланс в двигателе
при такой схеме замещения может быть представлен векторной диаграммой (рис. 25)
и системой уравнений
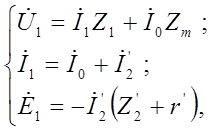
где ![]() - фазное напряжение статорной обмотки;
- фазное напряжение статорной обмотки; ![]() - соответственно эдс фазы статора и
неподвижного ротора;
- соответственно эдс фазы статора и
неподвижного ротора; ![]() - соответственно ток статора,
ток намагничивания; приведенный ток ротора;
- соответственно ток статора,
ток намагничивания; приведенный ток ротора; ![]() -
соответственно полное сопротивление фазы обмотки статора, полное сопротивление
магнитной цепи двигателя; полное приведенное сопротивление цепи обмотки
статора;
-
соответственно полное сопротивление фазы обмотки статора, полное сопротивление
магнитной цепи двигателя; полное приведенное сопротивление цепи обмотки
статора; ![]() - приведенное сопротивление,
эквивалентное механической нагрузке двигателя.
- приведенное сопротивление,
эквивалентное механической нагрузке двигателя.
При
вынесении контура намагничивания на напряжение статора (рис. 26) схема
замещения асинхронного двигателя приводится к двум независимым контурам,
включенным параллельно на напряжение ![]() : 1)
намагничивающего контура с сопротивлением
: 1)
намагничивающего контура с сопротивлением ![]() и
током
и
током ![]() ; 2) рабочего контура с
сопротивлением
; 2) рабочего контура с
сопротивлением ![]() и током
и током ![]() , где
, где 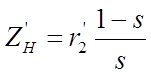 -
приведенное к первичной обмотке сопротивление, эквивалентное механической
нагрузке ротора двигателя;
-
приведенное к первичной обмотке сопротивление, эквивалентное механической
нагрузке ротора двигателя; 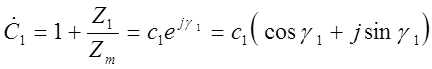 - комплексный
коэффициент, который представляет собой отношение вектора подводимого к двигателю
напряжения
- комплексный
коэффициент, который представляет собой отношение вектора подводимого к двигателю
напряжения ![]() к вектору эдс на зажимах
намагничивающего контура при синхронном вращении
к вектору эдс на зажимах
намагничивающего контура при синхронном вращении ![]() При
практических расчетах составляющие комплекса определяются по зависимостям:
При
практических расчетах составляющие комплекса определяются по зависимостям:
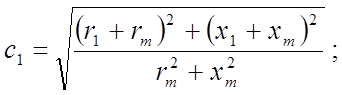
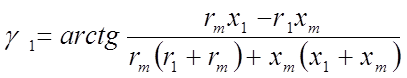 ,
,
где 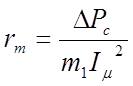 - активное сопротивление контура
намагничивания;
- активное сопротивление контура
намагничивания; 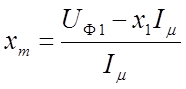 - реактивное сопротивление
контура намагничивания;
- реактивное сопротивление
контура намагничивания; ![]() - потери в стали
(расчет
- потери в стали
(расчет ![]() приводится ниже).
приводится ниже).
В
результате электрические и механические нагрузки электродвигателя при заданных
значениях ![]() и
и ![]() могут
быть рассчитаны по системе уравнений:
могут
быть рассчитаны по системе уравнений:
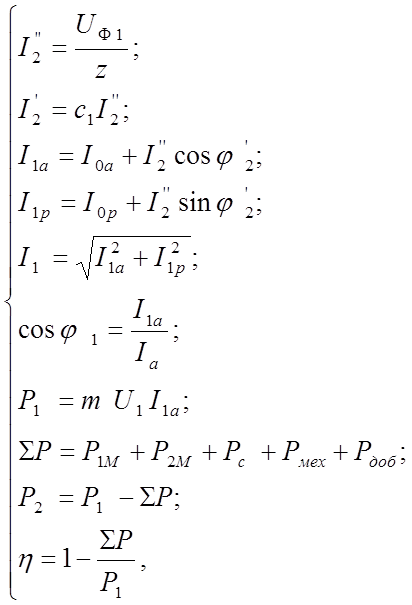
где I1 - ток обмотки статора; I’2 - приведенный ток ротора; I‘’2 - расчетный ток ротора; ![]() - полное сопротивление по схеме
замещения:
- полное сопротивление по схеме
замещения: 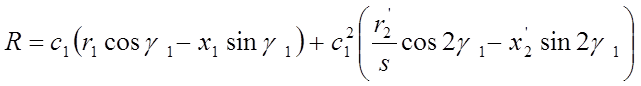 - активное сопротивление по схеме
замещения;
- активное сопротивление по схеме
замещения; 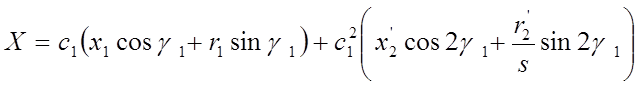 - реактивное сопротивление по схеме
замещения; I1
a ,I1
p -
активная и реактивная
составляющие тока статора;
- реактивное сопротивление по схеме
замещения; I1
a ,I1
p -
активная и реактивная
составляющие тока статора; ![]() - коэффициент
мощности;
- коэффициент
мощности; 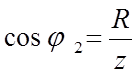 ;
; 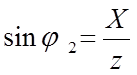 ;
Р 1 - мощность, подведенное к статорной
обмотке; SDР - суммарные потери;
;
Р 1 - мощность, подведенное к статорной
обмотке; SDР - суммарные потери; ![]() -
электрические потери в обмотке статора ;
-
электрические потери в обмотке статора ; ![]() -
электрические потери в стержнях ротора ;
-
электрические потери в стержнях ротора ; ![]() -
основные потери в стали;
-
основные потери в стали; ![]() - механические потери ;
- механические потери ; ![]() - добавочные потери от основной и от
высших гармонических составляющих тока;
- добавочные потери от основной и от
высших гармонических составляющих тока; ![]() -
кпд ТАД.
-
кпд ТАД.
Основные
потери в стали статора складываются из потерь в ярме (![]() ) и в зубцовом слое (
) и в зубцовом слое (![]() ) :
) :
![]() ,
,
где СП=(2,7...3,0) - коэффициент пульсаций, учитывающий добавочные потери от зубцовых гармонических индукции, т.е. добавочные потери холостого хода.
Потери
в стали ярма статора и зубцовом слое статора определяются соответственно как ![]() где
где 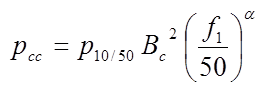 и
и
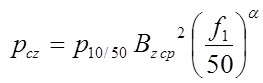 - удельные потери в ярме и зубцовом
слое статора ;
- удельные потери в ярме и зубцовом
слое статора ; ![]() - удельные потери в стали
при частоте перемагничивания 50 Гц;
- удельные потери в стали
при частоте перемагничивания 50 Гц; ![]() - индукция в ярме
статора ;
- индукция в ярме
статора ; ![]() - индукция в зубцовом слое статора;
- индукция в зубцовом слое статора; ![]() - вес ярма и зубцов статора.
- вес ярма и зубцов статора.
Основными потерями в стали ротора можно пренебречь, т.к. даже при номинальном абсолютном скольжении они очень малы.
Характеристикой
холостого хода АТД является зависимость ![]() при
при
![]() . Фактическое значение
. Фактическое значение ![]() рассчитывается по его активной
рассчитывается по его активной ![]() и реактивной
и реактивной ![]() составляющим:
составляющим:
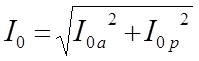 .
.
Определение
величин ![]() и
и ![]() выполняется
после расчета магнитной цепи двигателя и потерь в ней:
выполняется
после расчета магнитной цепи двигателя и потерь в ней: ![]() ;
;
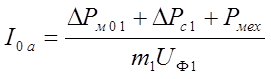 , где
, где ![]() -
электрические потери в обмотке статора на холостом ходу.
-
электрические потери в обмотке статора на холостом ходу.
Сложный
гармонический состав ![]() учитывается при расчете
добавочных потерь двигателя, т.к. именно эти потери учитывают наличие
«паразитных» токов и моментов.
учитывается при расчете
добавочных потерь двигателя, т.к. именно эти потери учитывают наличие
«паразитных» токов и моментов.
Для
определения токов отдельных гармонических используется метод «гармонических
двигателей», разработанный А.Я. Бергером и основанный на принципе наложения. АТД
представляют в виде ряда «гармонических» двигателей со своими схемами
замещения (рис. 27), имеющих общий вал. Каждый такой двигатель питается
напряжением своей гармоники, частота которой![]() ,
и для каждого двигателя рассчитываются ток, потери, момент, а результаты
суммируются. Высшие гармоники тока в трехфазной системе образуют вращающиеся
магнитные поля. Число полюсов этих полей и полюсное деление равны числу полюсов
и полюсному делению основного поля, а их частота вращения в ν раз больше
основной частоты
,
и для каждого двигателя рассчитываются ток, потери, момент, а результаты
суммируются. Высшие гармоники тока в трехфазной системе образуют вращающиеся
магнитные поля. Число полюсов этих полей и полюсное деление равны числу полюсов
и полюсному делению основного поля, а их частота вращения в ν раз больше
основной частоты ![]() где
где 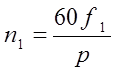 - частота вращения основной
гармонической магнитного поля статора, а скольжения роторов «гармонических
двигателей»определяется зависимостью
- частота вращения основной
гармонической магнитного поля статора, а скольжения роторов «гармонических
двигателей»определяется зависимостью 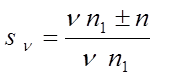 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.