-
магнитная индукция в ярме статора 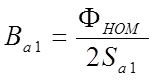 ;
;
-
магнитная индукция в характерных сечениях зубцов статора 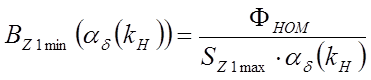 ;
; 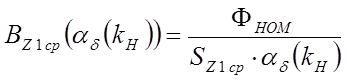 ;
;
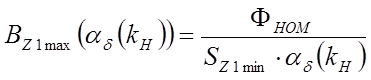 ;
;
-
магнитная индукция в воздушном зазоре 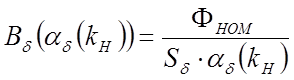 ;
;
-
магнитная индукция в характерных сечениях зубцов ротора 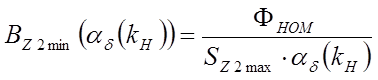 ;
; 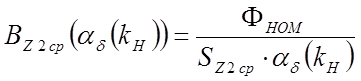 ;
;
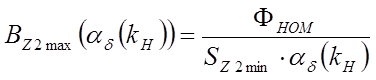 ;
;
-
магнитная индукция в ярме ротора 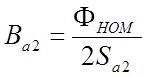 ,
,
где ![]() ,
, ![]() -
активные сечения магнитопроводов ротора и статора на один полюс;
-
активные сечения магнитопроводов ротора и статора на один полюс; ![]() - сечение воздушного зазора на один
полюс;
- сечение воздушного зазора на один
полюс; ![]() - активные сечения магнитопроводов в
зубцах статора на один полюс соответственно у основания в его среднем сечении и
коронке (рис. 19);
- активные сечения магнитопроводов в
зубцах статора на один полюс соответственно у основания в его среднем сечении и
коронке (рис. 19); ![]() - аналогичные сечения
магнитопровода в зубцах ротора (рис. 20). Все активные сечения магнитопроводов
статора и ротора рассчитываются аналогично ТЭД (табл. 5). Напряженности
магнитной цепи в зубцах и воздушном зазоре при аналитическом задании кривой
намагничивания и использовании формулы Симпсона должны представляться в виде
функций от
- аналогичные сечения
магнитопровода в зубцах ротора (рис. 20). Все активные сечения магнитопроводов
статора и ротора рассчитываются аналогично ТЭД (табл. 5). Напряженности
магнитной цепи в зубцах и воздушном зазоре при аналитическом задании кривой
намагничивания и использовании формулы Симпсона должны представляться в виде
функций от ![]() :
:
- в ярме статора и ротора ![]() ;
; ![]()
- в зубцах статора и ротора
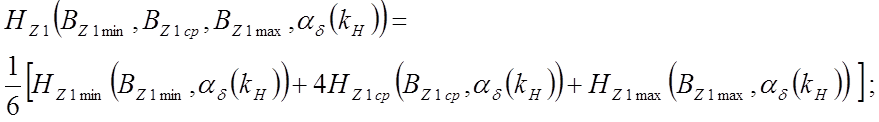
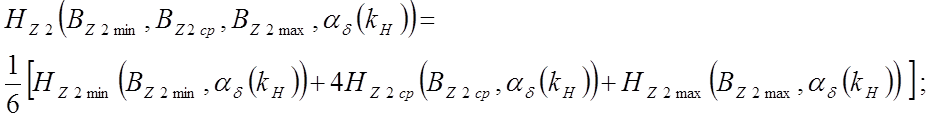
-
в воздушном зазоре 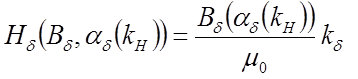 ,
где
,
где ![]() -результирующий коэффициент Картера,
учитывающий дополнительное сопротивление магнитной цепи в воздушном зазоре,
вносимое наличием пазов статора и ротора.
-результирующий коэффициент Картера,
учитывающий дополнительное сопротивление магнитной цепи в воздушном зазоре,
вносимое наличием пазов статора и ротора.
Значение коэффициента Картера определяется через аналогичные величины, рассчитанные отдельно для пазов статора и ротора:
![]() ,
,
где
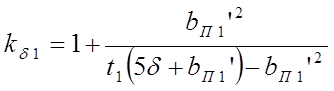 - коэффициент Картера, учитывающий
влияние пазов статора на магнитное сопротивление в воздушном зазоре;
- коэффициент Картера, учитывающий
влияние пазов статора на магнитное сопротивление в воздушном зазоре;
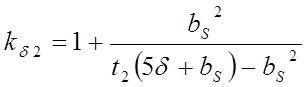 - коэффициент Картера, учитывающий
влияние пазов ротора на магнитное сопротивление в воздушном зазоре;
- коэффициент Картера, учитывающий
влияние пазов ротора на магнитное сопротивление в воздушном зазоре;
![]() - ширина паза статора в штампе (рис.
19);
- ширина паза статора в штампе (рис.
19);
![]() - ширина шлица паза ротора (рис.
20).
- ширина шлица паза ротора (рис.
20).
Решение нелинейного уравнения
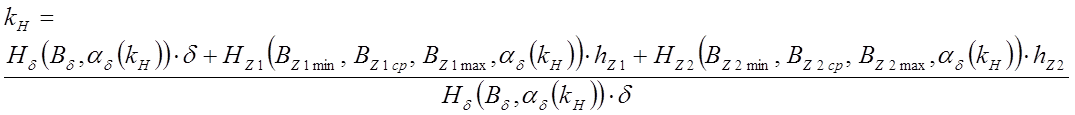 позволяет определить фактическое
значение коэффициента насыщения магнитной цепи
позволяет определить фактическое
значение коэффициента насыщения магнитной цепи ![]() для
каждого значения магнитного потока и соответствующее значение коэффициента
полюсного перекрытия
для
каждого значения магнитного потока и соответствующее значение коэффициента
полюсного перекрытия 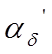 .
.
Таким образом, падения магнитного напряжения будут рассчитываться по зависимостям:
-
в зубцах статора 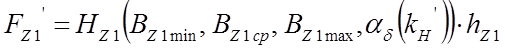 ;
;
-
в зубцах ротора 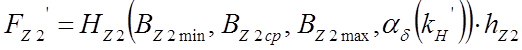 ;
;
-
в воздушном зазоре ![]() .
.
При определениинапряженностей в ярме статора и ротора должна учитываться
неравномерность распределения индукций в этих сечениях.. Как правило, это
учитывается коэффициентом неравномерности индукции вдоль силовой линии в ярме ![]() (рис. 21), поэтому падения
магнитного напряжения на участках ярма статора и ротора будут рассчитываться
соответственно по зависимостям:
(рис. 21), поэтому падения
магнитного напряжения на участках ярма статора и ротора будут рассчитываться
соответственно по зависимостям: ![]() и
и ![]() , где
, где ![]() и
и ![]() - длины магнитных силовых линий в
статоре и роторе, которые рассчитываются аналогично ТЭД (табл. 5).
- длины магнитных силовых линий в
статоре и роторе, которые рассчитываются аналогично ТЭД (табл. 5).
Требуемое значение намагничивающей силы на один полюс для создания магнитного
потока значением ![]() при холостом ходе АТД
при холостом ходе АТД
![]() ,
,
а действующее значение тока намагничивания на холостим ходу
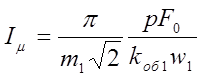 .
.
После расчета требуемого значения ![]() следует
определить его относительное значение
следует
определить его относительное значение 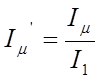 ,
которое на номинальном режиме должно составлять
,
которое на номинальном режиме должно составлять ![]() .
Если
.
Если ![]() целесообразно увеличить индукции в
сечениях за счет уменьшения габарита АТД. Если
целесообразно увеличить индукции в
сечениях за счет уменьшения габарита АТД. Если ![]() следует
уменьшить индукцию в наиболее напряженном сечении за счет увеличения его
площади. Если все участки магнитопровода имеют большое магнитное напряжение, то
целесообразно увеличить значение
следует
уменьшить индукцию в наиболее напряженном сечении за счет увеличения его
площади. Если все участки магнитопровода имеют большое магнитное напряжение, то
целесообразно увеличить значение ![]() .
.
Поскольку АТД работает при ![]() , то для определения его
характеристик холостого хода и рабочих характеристик требуется выполнять расчет
магнитной цепи для всего диапазона значений магнитного потока
, то для определения его
характеристик холостого хода и рабочих характеристик требуется выполнять расчет
магнитной цепи для всего диапазона значений магнитного потока ![]() .
.
По значению ![]() можно
оценить значение тока холостого хода
можно
оценить значение тока холостого хода ![]() . При работе без
нагрузки активная составляющая этого тока
. При работе без
нагрузки активная составляющая этого тока ![]() .
Поэтому можно считать, что ток холостого хода приблизительно равен своей
реактивной составляющей, т.е. току намагничивания
.
Поэтому можно считать, что ток холостого хода приблизительно равен своей
реактивной составляющей, т.е. току намагничивания ![]() .
.
Расчет
индуктивных сопротивлений. Индуктивные сопротивления
АТД рассчитываются на основании зависимости эдс рассеяния катушки. Основная
реактивность фазы обмотки определяется как ![]() ,
где
,
где ![]() - индуктивность рассеяния одной
катушки.
- индуктивность рассеяния одной
катушки.
На практике расчет реактивных сопротивлений
выполняется для характерных сечений катушки: пазовой и лобовой, а также по
коронкам зубцов ярма (дифференциальное рассеяние). С учетом такой
дифференциации, и того, что число витков в одной фазе статора ![]() реактивное сопротивление обмотки
статора представляется как
реактивное сопротивление обмотки
статора представляется как 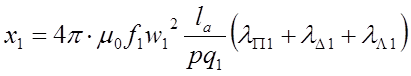 , где
, где ![]() ,
,![]()
![]() - проводимости рассеяния
соответственно пазовой и лобовой частей обмотки и по коронкам зубцов. Значения
проводимостей рассеяния определяются геометрией паза и катушки обмотки статора.
- проводимости рассеяния
соответственно пазовой и лобовой частей обмотки и по коронкам зубцов. Значения
проводимостей рассеяния определяются геометрией паза и катушки обмотки статора.
Проводимость пазового рассеяния обмотки статора при прямых пазах (рис.
22) 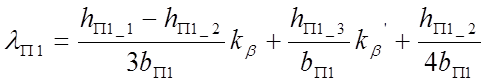 , где значения
, где значения ![]() ,
, ![]() ,
, ![]() принимаются по поверхности меди
проводников обмотки;
принимаются по поверхности меди
проводников обмотки;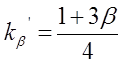 ;
; ![]() .
.
Проводимость дифференциального рассеяния обмотки статора
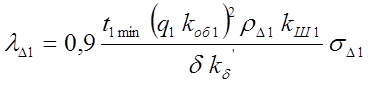 , где
, где 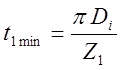 –
зубцовый шаг по внутреннему диаметру статора;
–
зубцовый шаг по внутреннему диаметру статора; ![]() -
коэффициент демпфирования (табл. 8);
-
коэффициент демпфирования (табл. 8); 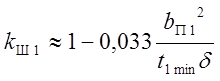 - коэффициент
учета открытия паза;
- коэффициент
учета открытия паза; ![]() - коэффициент Картера
(коэффициент воздушного зазора);
- коэффициент Картера
(коэффициент воздушного зазора);
![]() - коэффициент дифференциального
рассеяния (рис. 23).
- коэффициент дифференциального
рассеяния (рис. 23).
Таблица 8
|
|
|||||||||||
|
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|||||
|
3 |
0,92 |
0,87 |
0,84 |
0,78 |
0,68 |
||||||
|
4 |
0,90 |
0,81 |
0,77 |
0,75 |
0,72 |
0,67 |
|||||
|
5 |
0,78 |
0,71 |
0,69 |
0,67 |
0,65 |
0,62 |
|||||
|
6 |
0,73 |
0,67 |
0,62 |
0,60 |
0,58 |
0,57 |
|||||
|
8 |
0,66 |
0,58 |
0,52 |
0,49 |
0,47 |
0,46 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.