Анализ инвестиционного проекта по интегральным показателям (NPV, IRR, PI, PB), страница 5

Таблица 14. Интегральные пок-ли, соответствующие новой стоимости установки для фирмы Б.

Изменение стоимости установки практически никак не сказывается на интегральных показателях. Это очевидно, потому что в смете затрат, стоимость установки составляет всего 3000 рублей, а это всего 3%.

ЧАСТЬ III. ФОРМИРОВАНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ ИП

Если анализ устойчивости даёт численное значение некого интегрального показателя при варьировании какого-либо параметра, то область устойчивости – это, прежде всего, графическое представление варьирования параметров проекта. Область устойчивости показывает, на какую предельную величину можно изменить тот или иной показатель, чтобы при этом проект оставался эффективным. Математическая модель представлена ниже:

Предположим, что доход, стоимость оборудования и стоимость установки могут измениться на некоторую величину  q₁%,  q₂%,  q₃% соответственно:

(1)          

(2)               где

(3)                где

    Решая эти три уравнения при разных значениях ставки дисконтирования, получим значения параметров q₁%,  q₂%,  q₃%. Откладывая их на координатной сетке, получим объёмную фигуру.

.

График 1. Область устойчивости фирмы А

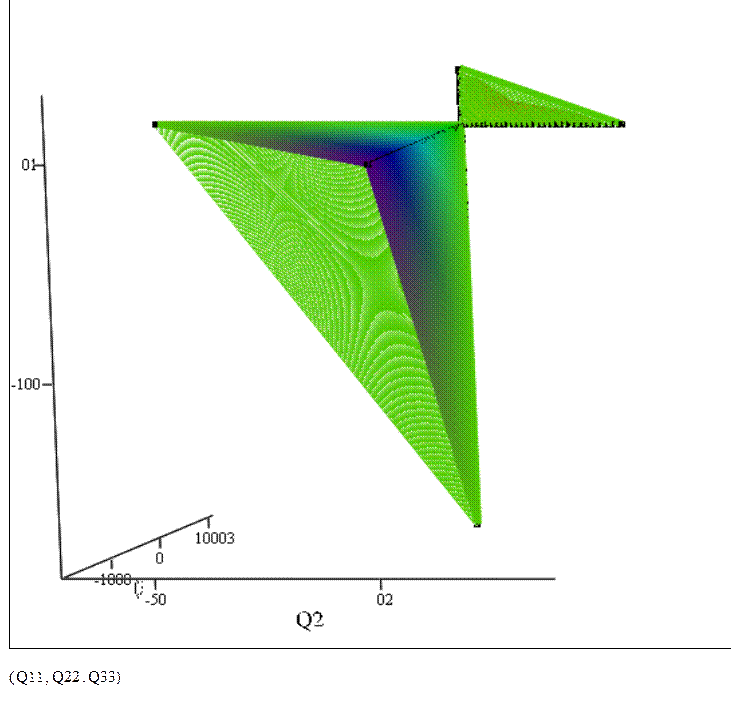
График 2. Область устойчивости фирмы Б.

     Ставка дисконтирования, соответствующая точке, в которую сходится область устойчивости, равна внутренней доходности проекта. Область устойчивости проекта находится внутри фигуры. Однако это справедливо тогда, когда значения параметров q_iполучены при ставке дисконта, которая меньше IRR. В противном случае, область устойчивости находится вне фигуры.

ПРИЛОЖЕНИЕ 1

Расчёт IRR производился в математическом редакторе Mathcad 11. Решалось уравнение (2) относительно нужного показателя, обозначенного за х. Для наглядности представления был построен график зависимости функции (NPV) от нужной переменной (IRR или х), на котором отчётливо видно, что точка пересечения  NPV с осью абсцисс уходит на бесконечность.  Это, в частности, означает, что IRR равен бесконечности.

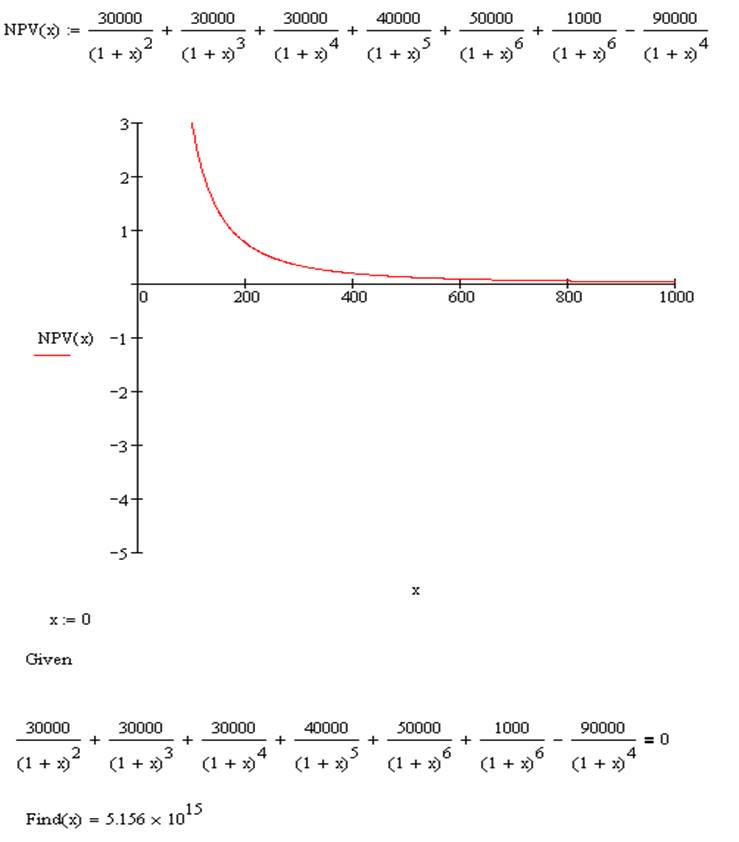
Под графиком отдельно решено это уравнение, решение которого ещё раз доказывает верность полученного ответа. В теории же существует объяснение этому явлению, дело в том, что в данном случае проект имеет необычные денежные потоки, потому что исходящий поток денежных средств (капиталовложения) происходит в некоторый момент по ходу реализации проекта. Проекты с необычными потоками денежных средств представляют особую сложность. Проблема состоит в том, что полученное значение IRR является бессмысленным (как в нашем случае). Бывает даже так, что проблема состоит в множественности IRR (в нашем случае это имеет место, когда затраты вносятся на протяжении 6 лет). Решение этой проблемы на практике заключается в вычислении показателя, носящего название модифицированная внутренняя доходность (MIRR). Однако в рамках нашего курса она не изучалась и не рассматривалась, поэтому затрагивать её мы не беремся, однако заметим, что она решает проблему множественности ставок и считается, что это лучший показатель действительной рентабельности проекта.  

ПРИЛОЖЕНИЕ 2

Здесь будем полагать, что ставка дисконта не остаётся постоянной, а увеличивается с каждым годом:

Таблица 15. Значение дисконтной ставки