Теория систем линейных алгебраических уравнений

220400                   Алгебра и геометрия                    Толстиков А.В.

Лекции 12. Теория систем линейных алгебраических уравнений.

План

1.  Теорема Кронекера-Капелли.

2.  Однородная система линейных уравнений Фундаментальная система решений

3.  Структура решений системы линейных уравнений.

Рекомендуемая литература

1.  Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.

2.  Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997.

3.  Воеводин В.В. Линейная алгебра.. М.: Наука 1980.

4.  Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П.. М.: Наука, 1981.

5.  Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.

6.  Воеводин В.В. Линейная алгебра. М.: Наука, 1980.

1. Теорема Кронекера-Капелли. Рассмотрим систему линейных  уравнений (СЛУ)

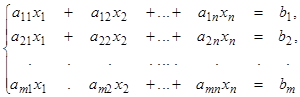                                                                (1)

с коэффициентами и свободными членами из поля Р. Пусть

 , 

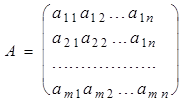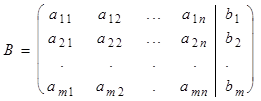
матрица и расширенная матрица системы (1).

Столбцы матриц А и В являются векторами в пространстве матриц Р^n´1 :

a₁ = , a₂ = , ..., a_n = , b = .

Используя эти обозначения и определения операций над матрицами получим, что

 b =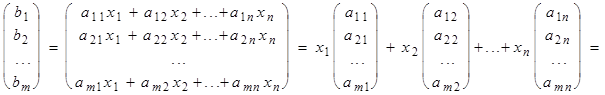

= x₁a₁ + x₂a₂ + ...+ x_na_n.

Тогда систему линейных уравнений (1) можно записать в следующей векторной форме:

x₁a₁ + x₂a₂ + ...+ x_na_n = b .                                                                             (2)

Легко показать, что система (1) равносильна векторному уравнению (2).

Теорема 1 (теорема Кронекера-Капелли). (СЛУ) (1) разрешима тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы. При этом, если rangA = n , то система (1) имеет единственное решение, если rangA < n , то система (1) имеет бесконечно много решений, если поле Р.

Л.Кронекер (1823-1891) - немецкий математик, А.Капелли (1855-1910) - итальянский математик.

Доказательство. Столбцы матриц А и В являются векторами в пространстве матриц Р^n´1 :

a₁ = , a₂ = , ..., a_n = , b = .

По следствию из теоремы о ранге матрицы ранги матриц А и В равны соответственно рангам систем векторов

a₁, a₂, ..., a_n,                                                                                    (3)

и

a₁, a₂, ..., a_n, b .                                                                                 (4)

1. Необходимость. Пусть система (1) разрешима и (b₁, b₂, ...,b_n) ее решение. Тогда справедлива система верных числовых равенств

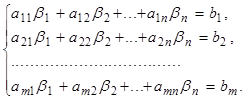
Отсюда следует векторное равенство:

b =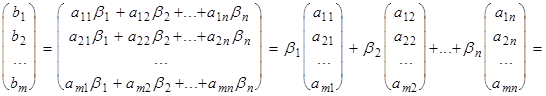

= b₁a₁ + b₂a₂ + ...+ b_na_n.

Тогда каждый вектор системы (4) линейная комбинация векторов системы (3). Действительно,  это следует из указанного выше равенства и из равенств

a_i = 0×a₁ + ... + 0×a_i-1 + 1× a_i + 0×a_i+1 + ... + 0×a_n , i =1, 2, ...,n .

Из равенств

a_i = 0×a₁ + ... + 0×a_i-1 + 1× a_i + 0×a_i+1 + ... + 0×a_n + 0×b , i =1, 2, ...,n, получаем, что каждый вектор системы (3) линейная комбинация векторов системы (4). Таким образом системы векторов (3) и (4) эквивалентны и поэтому их ранги равны. Следовательно, rangA = rang(3) = rang(4) = rangB.

2. Достаточность. Пусть rangA = rangB = r. Тогда  ранги систем векторов (3) и (4) равны r . По определению ранга система векторов (3) обладает базисом, состоящим из r векторов. Можно предположить, что базис образуют первые r векторов

a₁, a₂, ..., a_r ,                                                 (5)

в противном случае вектора и соответственно переменные можно перенумеровать. Тогда по теореме о базисах система (5) является базисом  и системы векторов (4). Но тогда вектор b системы векторов (4) линейно выражается через систему (5):

 b = b₁a₁ + b₂a₂ + ...+ b_ra_r = b₁a₁ + b₂a₂ + ...+ b_ra_r +  0×a₂ + ...+ 0×a_r.

Тогда набор чисел (b₁, b₂, ..., b_r, 0, ..., 0) решение системы (1) и она разрешима.

Пусть rangA = n , т.е. r = n . Тогда система векторов (3) является базисом системы векторов (4) и вектор b единственным образом линейно выражается через вектора системы (3). Тогда векторное уравнение (2) и поэтому система (1) имеет единственное решение.