Пусть rangA < n , т.е. r < n . Так как система векторов (5) базис системы (4), то каждый из векторов b, ar+1, ...,an линейная комбинация векторов системы (5). Тогда для любых чисел br+1, ... , bn Î P вектор b - br+1ar+1 - ...- bnan линейная комбинация векторов системы (5):
b - br+1ar+1 - ...- bnan = b1a1 + b2a2 + ...+ brar.
Отсюда b1a1 + b2a2 + ...+ brar + br+1ar+1 + ...+ bnan = b и набор чисел (b1, b2, ..., br, br+1, ..., bn) решение системы (1). Если поле P бесконечно, то набор чисел br+1, ... , bn можно выбрать бесконечным числом способов и поэтому система (1) имеет бесконечно много решений. Если поле P содержит q элементов, то набор чисел br+1, ... , bn можно выбрать qn-r способами и система (1) имеет qn-r решений.
2. Однородная система линейных уравнений (ОСЛУ). Пусть дана однородная система m линейных уравнений с n неизвестными:
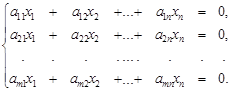 (2)
(2)
Каждое решение системы (2) вектор в арифметическом n-мерном пространстве Рn. Очевидно, что нулевой вектор 0 = (0, 0, ...,0) является решением системы (1). Обозначим через Х0 множество решений системы (1). Тогда имеет место следующая теорема о структуре множества решений однородной системы линейных уравнений.
Определение 1. Подмножество L ¹ Æ векторного пространства V называется подпространством V, если
1) (" a, b Î L) a + b Î L; 2) (" a Î L) (" a Î R) aa Î L.
.Теорема 2. Множество Х0всех решений ОСЛУ (2) образует подпространство размерности n - r арифметического n-мерного пространстве Рn, где n - число неизвестных в системе, r - ранг матрицы системы.
Доказательство. В силу сказанного выше Х0 Í Рn , Х0 ¹ Æ . Пусть вектора a = (a1,a2, ..., an), b = (b1,b2, ..., bn) Î Х0. Тогда по определению выполняются следующие системы верные равенства:
ai1a1 + ai2a2 + ... + ainan = 0, i = 1, 2, ...,m; (7)
ai1b1 + ai2b2 + ... + ainbn = 0, i = 1, 2, ...,m. (8)
К каждому равенству системы (7) прибавим почленно соответствующее равенство системы (8) и получим систему верных числовых равенств:
ai1(a1 + b1) + ai2(a2 + b2) + ... + ain(an + bn) = 0, i = 1, 2, ...,m,
из которой по определению следует, что вектор a + b = (a1 + b1,a2 + b2, ..., an + bn) решение системы (6) , т.е. a + b Î Х0.
Умножая обе части равенств (8) на произвольное число g Î Р получаем систему верных числовых равенств:
ai1(ga1) + ai2(ga2) + ... + ain(gan) = 0, i = 1, 2, ...,m.
Отсюда следует, что для любого вектора a Î Х0 и любого числа g Î Р вектор ga Î Х0 . Таким образом по определению Х0 подпространство векторного пространства Рn .
Пусть r =rangA . Докажем, что dimХ0 = n - r. Для этого решая систему (6) методом Гаусса приведем ее с помощью элементарных преобразований и преобразований вычеркивания нулевых уравнений к ступенчатому виду. При этом матрица системы с помощью элементарных преобразований строк и преобразований вычеркивания нулевых строк перейдет к матрице ступенчатого вида, которая будет содержать r строк. При этом в полученной системе ступенчатого вида будет r уравнений. Будем предполагать, что главными неизвестными в полученной системе ступенчатого вида будут первые r неизвестных x1, x2, ..., xr и полученная система имеет вид:
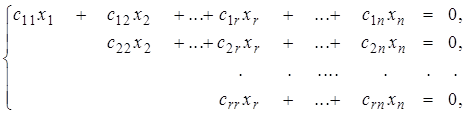 (9)
(9)
где все коэффициенты с11 , с22 , ..., сrr не равны нулю, неизвестные x1, x2, ..., xr - главные, а неизвестные xr+1, ..., xn - свободные. Пусть xr+1 = ar+1 , ..., xn = an , где ai Î P , i = r+1, ...,n. Из уравнений системы (9) выразим значения главных неизвестных через свободные и получим:
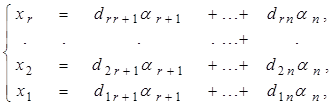
где dij Î P; i = 1, 2, ..., r; j = r + 1, ..., n. Запишем общее решение системы (6) в виде вектор-столбца:
xT
= 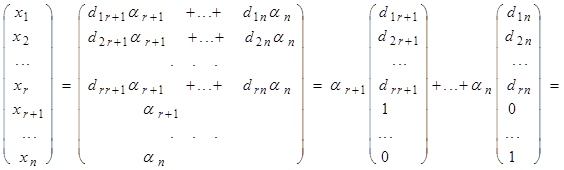
=ar+1x1T + ...+ anxn-rT.
Таким образом каждое решение системы (6) линейная комбинация n-r решений:
x1 = (d1r+1, d2r+1, ..., drr+1, 1, ..., 0), ..., xn-r = (d1n, d2n, ..., drn, 0, ..., 1). (10)
Рассмотрим матрицу, составленную из координат этих векторов,
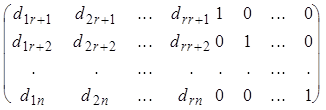 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.