Так как ранг этой матрицы равен n-r , то строки ее линейно независимы и система векторов (10) линейно независима и по определению базиса она образует базис подпространства Х0 решений однородной системы (6). Следовательно, dim Х0 = n-r . Теорема доказана.
Определение 1. Фундаментальной системой решений однородной системы называется базис подпространства решений системы.
Следствие 1. Любая однородная система линейных уравнений обладает фундаментальной системой решений, состоящей из n-r решений.
Если x1, x1, ..., xn-r - фундаментальная система решений однородной системы (6), то она обладает свойствами:
1) она линейно независима,
2) любое решение x системы (6) единственным образом представляется в виде x = ar+1x1 + ar+2x2 + ...+ anxn-r; ai Î P, i = r+1, ...,n.
Далее множество решений Х0 однородной системы есть линейная оболочка натянутая на фундаментальную систему решений:
Х0 =L(x1, x1, ..., xn-r).
Фундаментальную систему решений однородной системы можно найти по методу, изложенному в доказательстве теоремы 2.
Пример 1.
Найти фундаментальную систему решений системы![]()
![]()
Приведем систему элементарными преобразованиями к ступенчатому виду:
![]()
Пусть x3 = a , x4 = b. Тогда х2 = -2a - 3b , х1 = -a - 2b . Отсюда общее решение системы
хТ
= 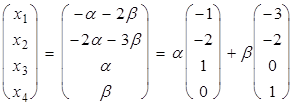 , и фундаментальная система
решений: х1 = (-1,
-2, 1, 0), х2
= (-2, -3,
0, 1).
, и фундаментальная система
решений: х1 = (-1,
-2, 1, 0), х2
= (-2, -3,
0, 1).
По доказанной теореме однородная система имеет только нулевое решение тогда и только тогда, когда размерность подпространства ее решений равна 0, т.е. при n-r = 0, n =r , определитель системы не равен нулю. Тогда получаем следствия.
Следствие 2. Однородная система n линейных уравнений c n неизвестными имеет только одно нулевое решение тогда и только тогда когда определитель системы не равен нулю.
Следствие 3. Однородная система n линейных уравнений c n неизвестными имеет ненулевое решение тогда и только тогда когда определитель системы равен нулю.
Рассмотрим СЛУ (1) и соответствующую ей ОСЛУ (2). Пусть Х - множество решений СЛУ (1) (называемое общим решением системы (1)), Х0 - множество решений ОСЛУ (2) - общее решение системы (2), c - данное решением СЛУ(1) - частное решение СЛУ (1).
Теорема 3. Общее решение Х СЛУ (1) равно сумме общего решения Х0 соответствующей СЛОУ (2) и частного решения c СЛУ (1) , т.е. справедливо равенство
Х = Х0 + х0. (3)
Доказательство. Пусть c = (g1,g2, ..., gn) - некоторое фиксированное решение системы (1), т.е. справедлива система верных числовых равенств:
ai1g1 + ai2g2 + ... + aingn = bi , i = 1, 2, ...,m. (4)
Докажем равенство (3). Пусть а = (a1,a2, ..., an) Î Х. Тогда имеем следующие верные равенства:
ai1a1 + ai2a2 + ... + ainan = bi , i = 1, 2, ...,m. (5)
Вычитая почленно их равенств (5) соответствующие равенства (4) получим систему верных равенств:
ai1(a1 - g1) + ai2(a2 - g2) + ... + ain(an - gn) = 0 , i = 1, 2, ...,m.
Из этой системы равенств следует, что вектор а - x0 = (a1-g1,a2 -g2, ...,an-gn) является решением системы (2), т.е. вектор b = а - x0 Î X0. Поэтому а = b + x0 Î Х0 + х0 и Х Í Х0 + х0.
Докажем обратное включение. Пусть а Î Х0 + х0. Тогда а = b + x0, где b Î Х0 . Пусть b = (b1,b2, ..., bn). Тогда
ai1b1 + ai2b2 + ... + ainbn = 0, i = 1, 2, ...,m. (6)
Прибавляя почленно к каждому их равенств (6) соответствующие равенства (4) получим систему верных равенств:
ai1(b1 + g1) + ai2(b2 + g2) + ... + ain(bn + gn) = bi , i = 1, 2, ...,m.
Отсюда следует, что вектор а = b + x0 = (b1 + g1, b2 + g2, bn + gn) является решением системы (1) и а Î Х. Поэтому Х0 + х0 Í Х. Следовательно, по определению равенства множеств Х = Х0 + х0.
Следствие 1. Любое решение x системы (1) единственным образом представляется в виде x = ar+1x1 + ar+2x2 + ...+ anxn-r + х0, где ai Î P, i = r+1, ...,n; x1, x1, ..., xn-r - фундаментальная система решений соответствующей с данной системы (2), х0 - какое-нибудь решение системы (1).
Следствие 2. Совместная СЛУ имеет единственное решение тогда и только тогда, когда соответствующая ей система имеет единственное решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.