Докажем теперь, что каждая строка матрицы А линейная комбинация первых r строк. Проверим это для k-й строки (r + 1 £ k £. m) . Для этого рассмотрим определитель (2) (k + 1) - го порядка.
Определитель (2) при любом s (1 £ s £. n) равен нулю. Если 1 £ s £. r , то он имеет два равных столбца, и по свойству определителей равен нулю. Если r + 1 £ s £. n , то это минор (r + 1) - го порядка матрицы А и равен нулю по предположению. Разложим определитель (2) по элементам последнего столбца и получим:
a1sA1s + a2sA2s+ ... + arsArs + aksAks = 0, где A1k, A2k, ..., Ars, Aks - алгебраические дополнения соответствующих элементов в определителе (2). По определению алгебраического дополнения Aks = (-1)r+1+r+1×M = M ¹ 0, A1k, A2k, ..., Ars ни не зависят от s , т.е. от элементов s-го столбца матрицы А обозначим их . Тогда из последнего равенства находим:
.
Последнее равенство справедливо для всех s , 1 £ s £ n, и его коэффициенты не зависят от s. Это означает, что координаты вектора ak выражаются линейно с одними и теми же коэффициентами через соответствующие координаты векторов a1, a2, ..., ar. Поэтом вектор ak линейная комбинация векторов a1, a2, ..., ar .
Следовательно, первые r строк a1, a2, ..., ar матрицы А образуют базис системы всех строк матрицы . Поэтому rangА = r.
При транспонировании матрицы А ее миноры транспонируются и по свойства определителя не изменяются. Поэтому максимальные порядки миноров не равных нулю в матрица А и Аt равны. Отсюда rang A = rang Аt . Так как ранг матрицы А равен рангу системы строк матрицы А, а ранг матрицы Аt равен рангу системы столбцов матрицы А, то получаем следующее следствие.
Следствие 1. Строковый ранг матрицы равен ее столбцовому рангу.
В силу этого следствия строки и столбцы матрицы при вычислении ранга матрицы равноправны.
Следствие 2. Определитель квадратной матрицы А порядка n >1 равен нулю тогда и только тогда, когда какая-нибудь строка матрицы есть линейная комбинация остальных строк.
Доказательство. Достаточность следует из свойства определителя. Пусть detA =0. Тогда наибольший порядок r минора неравного нулю в матрице А меньше n . По теореме rang A = r . Так как r < n , то число базисных строк в матрице меньше n и по теореме о базисах строки матрицы А линейно зависимы. Поэтому хотя бы одна из строк матрицы А есть линейная комбинация остальных строк матрицы.
Следствие 3. Определитель квадратной матрицы А порядка n >1 равен нулю тогда и только тогда, когда какая-нибудь строки матрицы линейно зависимы.
Доказательство следует в силу свойств линейной зависимости и из следствия 2.
Определение 2. Минор М¢ (k + 1)-го порядка матрицы А называется окаймляющим минором для минора М k -го порядка той же матрицы, если все элементы минора М элементами минора М¢.
При r + 1 £ s £. n определитель (2) окаймляющий минор для минора М. Поэтому в ходе доказательства теоремы 1 мы установили еще следующую предложение.
Теорема 2. Если в ненулевой матрице А имеется минор r-го порядка отличный от нуля, а все окаймляющие его миноры равны нулю или не существуют, то ранг матрицы А равен r.
Из теоремы 2 вытекает метод вычисления ранга матрицы, называемый методом окаймления миноров. Для того, чтобы вычислить ранг ненулевой матрицы, выбирается любой элемент матрицы не равный нулю (минор первого порядка) и рассматриваются окаймляющие его миноры второго порядка. Если все эти окаймляющие миноры равны нулю или не существуют, то ранг матрицы равен двум. Если среди их есть минор не равный нулю, то рассматриваются окаймляющие его миноры третьего порядка.
Продолжая этот процесс, который закончится через конечное число шагов, мы найдем ранг матрицы А.
Пример 1. Вычислить ранг матрицы
.
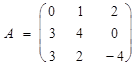Так как
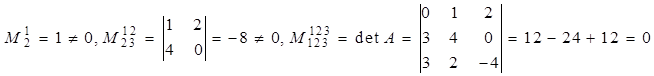, то rang A=2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.