Ранг системы векторов и ранг матрицы. Вычисление ранга матрицы, методом окаймления миноров, страница 2

a = a₁b₁ + a₂b₂ +...+ a_rb_r ; a₁, a₂, ...,a_n Π P,                                                         (1)

и такое представление единственно.

В силу 5° базис это максимально линейно независимая подсистема системы S, а ранг системы S число векторов в такой подсистеме.

Представление вектора a  в виде (1) называется разложением вектора по векторам базиса, а числа  a₁, a₂, ..., a_r называются координатами вектора a в данном базисе.

Доказательство. 1° Пусть b₁, b₂, ..., b_k - линейно независимая подсистема системы S. Если каждый вектор системы S линейно выражается через вектора нашей подсистемы, то по определению она является базисом системы S.

Если имеется вектор в системеS , который линейно не выражается через вектора b₁, b₂, ..., b_k, то обозначим его через  b_k+1 . Тогда системы b₁, b₂, ..., b_k, b_k+1 - линейно независима. Если каждый вектор системы S линейно выражается через вектора этой подсистемы, то по определению она является базисом системы S.

Если имеется вектор в системеS , который линейно не выражается через b₁, b₂, ..., b_k, b_k+1, то повторим рассуждения. Продолжая этот процесс, мы либо придем к базису системы S , либо увеличим число векторов в линейно независимой системе на единицу. Так как в системеS конечное число векторов, то вторая альтернатива не может продолжаться бесконечно и на некотором шаге получим базис системыS.

2° Пусть  S  конечная система векторов и S  ¹{0}.  Тогда в системе S есть вектор b₁ ¹ 0, который образует линейно независимую подсистему системы S . По первой части его можно дополнить до базиса системы S . Таким образом системаS обладает базисом.

3° Допустим, что система S имеет два базиса:

b₁, b₂, ..., b_r ,                                                                                      (2)

c₁, c₂, ..., c_s ,                                                                                       (3)

По определению базиса система векторов (2) линейно независима и (2) Í S . Далее по определению базиса каждый вектор системы (2) линейная комбинация векторов системы (3). Тогда по основной теореме о двух системах векторов r £ s. Аналогично доказавается, что s £ r. Из этих двух неравенств следует r = s.

4° Пусть r = rangS, a₁, a₂, ..., a_r - линейно независимая подсистема S. Покажем, что она является базисом систем S. Если она не является базисом, то по первой части ее можно дополнить до базиса и получим базис a₁, a₂, ..., a_r, a_r+1,..., a_r+t , содержащий более чем r векторов. Это противоречит доказанному в третьей части.

5° Если k  векторов a₁, a₂, ..., a_k (k > r) системы S - линейно независимы, то по первой части эту систему векторов  можно дополнить до базиса и получим базис a₁, a₂, ..., a_k, a_k+1,..., a_k+t , содержащий более чем r векторов. Это противоречит доказанному в третьей части.

6° Пусть b₁, b₂, ..., b_r базис системы S. По определению базиса любой вектор a Î S есть линейная комбинация векторов базиса:

a = a₁b₁ + a₂b₂ +...+ a_rb_r.

Доказывая единственность такого представления допустим противное, что есть еще одно представление:

a = b₁b₁ + b₂b₂ +...+ b_rb_r.

Вычитая равенства почленно находим

0 = (a₁ - b₁)b₁ + (a₂ - b₂)b₂ +...+ (a_r - b_r)b_r.

Так как базис b₁, b₂, ..., b_r линейно независимая система, то все коэффициенты a_i - b_i =0; i = 1, 2, ..., r. Следовательно, a_i = b_i ; i = 1, 2, ..., r и единственность доказана.

3. Эквивалентные системы векторов и их свойства.

Лемма 1. Пусть S₁ , S₂ - конечные системы векторов. Если вектор с  линейная комбинация векторов системы S₁ и каждый вектор системы S₁ линейная комбинация векторов системы S₂  , то вектор с линейная комбинация векторов системы S₂ .

Доказательство. Пусть S₁ = { a₁, a₂, ..., a_m } , S₂ = { b₁, b₂, ..., b_n } . По по условию:

с = a_i , a_i = 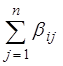b_j(i=1, 2,... , m).

Подставляя вторые равенства в первое получим:

с = (b_j) = b_j .

Лемма доказана.