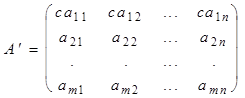Ранг системы векторов и ранг матрицы. Вычисление ранга матрицы, методом окаймления миноров, страница 4

, строки которой обозначим буквами a¢₁, a¢₂, ..., a¢_m . По определению 1

rangA =rang(a₁, a₂, ..., a_m) ,  rangA¢ =rang(a¢₁, a¢₂, ..., a¢_m).

Так как

a¢₁ = ca₁ = ca₁ + 0×a₂ + ...+ 0×a_m , a₁ = a¢₁ = a¢₁ + 0×a¢₂ + ...+ 0×a¢_m ,

a¢₂ = a₂ = 0×a₁ + 1×a₁ + ...+ 0×a_m , a₁ = a¢₁ = 0×a¢₁ + 1×a¢₁ + ...+ 0×a¢_m ,

.  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .

a¢_m = a_m = 0×a₁ + 0×a₁ + ...+ 1×a_m , a_m = a¢_m = 0×a¢₁ + 0×a¢₁ + ...+ 1×a¢_m , то системы векторов a₁, a₂, ..., a_m и a¢₁, a¢₂, ..., a¢_m эквивалентны и по теореме 4.3 rang(a₁, a₂, ..., a_m) = rang(a¢₁, a¢₂, ..., a¢_m). Поэтому rangA = rangA¢.

Аналогичным образом доказывается, что ранг матрицы не меняется при прибавлении к одной строке матрацы другой, умноженной на любое число c Î Р, и не меняется при выбрасывании нулевой строки.

Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида и при этом ранг исходной матрицы будет равен числу строк в поученной матрице ступенчатого вида.

Доказательство.   По теореме 2.1.1.1 любую ненулевую матрицу конечным числом элементарных преобразований и преобразований, выбрасывания нулевой строки можно привести к матрице ступенчатого вида:

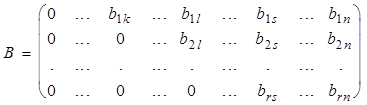, где b_1k ¹ 0, b_2l ¹ 0, ..., b_rs ¹ 0. По теореме 1 rangA = rangB. Покажем, что rangВ = r, а для этого докажем, что строки b₁, b₂, ..., b_r матрицы B линейно независимы. Действительно, если найдутся такие числа a₁, a₂, ..., a_r Î Р, что выполняется равенство

a₁b₁ + a₂b₁ + ...+ a_rb_r   = 0, то, переходя от векторного равенства к равенствам соответствующих координат векторов, стоящих в правой и левой частях этого равенства, получаем систему n числовых равенств:

a₁×0 + a₂×0 + ...+ a_r×0   = 0,

.  .  .  .  .  .  .  .  .  .  .  .  .  .

a₁b_1k + a₂×0 + ...+ a_r×0   = 0,

.  .  .  .  .  .  .  .  .  .  .  .  .  .

a₁b_1l + a₂b_2l + ...+ a_r×0   = 0,

.  .  .  .  .  .  .  .  .  .  .  .  .  .

a₁b_1s + a₂b_2s + ...+ a_rb_rs = 0,

.  .  .  .  .  .  .  .  .  .  .  .  .  .

a₁b_1n + a₂b_2n + ...+ a_rb_rn = 0.

В силу того, что  b_1k ¹ 0 , b_2l ¹ 0 , ...,   b_rs ¹ 0  отсюда находим, что  a₁ = 0 , a₂ = 0 , ..., a_r = 0 . Следовательно, система векторов b₁, b₂, ..., b_r линейно независима и rangB =r. Поэтому и rangА =r. Теорема доказана.

Из теоремы 2 вытекает метод вычисления ранга матрицы, называемый методом элементарных преобразований. Для того, чтобы вычислить ранг матрицы мы матрицу элементарными преобразованиями и вычеркиванием нулевых строк приводим к ступенчатому виду. Тогда по теореме 2 ранг матрицы равен числу строк в полученной матрице ступенчатого вида.

Пример 1. Вычислить ранг матрицы

.

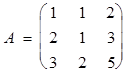Приводим матрицу А элементарными преобразованиями и вычеркиванием нулевых строк к ступенчатому виду

.

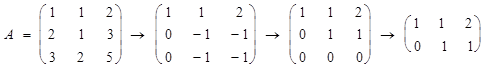5. Теорема о ранге матрицы и следствия и ее. Вычисление ранга матрицы методом окаймления миноров.

Теорема 1 (теорема о ранге матрицы). Ранг ненулевой матрицы равен максимальному порядку отличных от нуля миноров данной матрицы.

Доказательство. Пусть дана ненулевая матрица А размерности m´n. Тогда у этой матрицы есть миноры не равные нуля и среди миноров не равных нулю есть миноры максимального порядка. Через r обозначим наибольший порядок неравного нулю минора. Не нарушая общности будем считать, что ненулевой минор M r-го порядка находится в левом верхнем углу матрицы А (в противном случае строки и столбцы матрицы А можно не меняя ранг матрицы переставить) (см. (1). Тогда

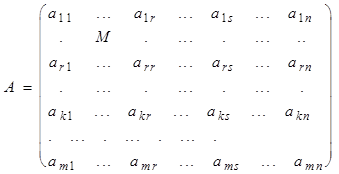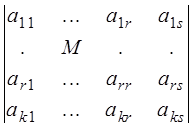.    (1)                                                  (2)                

Пусть a₁, a₂, ..., a_m  - строки матрицы. Первые r строк a₁, a₂, ..., a_r матрицы А линейно независимы. Действительно, если бы они были линейно зависимы, то по свойству 3.1 какая-нибудь из строк a₁, a₂, ..., a_r есть линейная комбинация остальных строк этой системы. Но тогда и в миноре М  соответствующая строка есть линейная комбинация остальных строк минора. Тогда по свойству определителя М = 0, а это противоречит выбору минора М.