Доказательство. Из определения произведения матриц следует, что столбцы матрицы AB являются линейными комбинациями столбцов матрицы A. Тогда столбцы матрицы AB выражаются через базисные столбцы матрицы A. И максимальное число линейно независимых столбцов матрицы AB меньше ранга матрицы A. Отсюда ранг матрицы AB не больше ранга матрицы A.
Из определения произведения матриц следует, что строки матрицы AB являются линейными комбинациями строк матрицы B. Тогда строки матрицы AB выражаются через базисные строки матрицы B. Отсюда ранг матрицы AB не больше ранга матрицы B.
Лемма 2. Если один из сомножителей A или B квадратная невырожденная матрица, то ранг произведения AB равен рангу другого сомножителя.
Доказательство. Пусть C = AB, и B - невырожденная матрица. По лемме 1 rang C £ {rang A, rang B}. Так как B - невырожденная матрица, то rang A £ rang B. Поэтому rang C £ rang A. Далее A = CB -1. Тогда rang A £ rang C. Следовательно, rang C = rang A.
Доказательство теоремы. Пусть квадратичная форма g получена из квадратичной формы f с помощью невырожденного преобразования переменных (2.4) с матрицей T. Тогда по теореме 2.2 С = TtBT., где B, С - матрицы соответственно квадратичных форм f и g. Так как матрица невырожденная, то по лемме 2 rang С = rang TtB = rang B.
Так как форма канонического вида получена из квадратичной формы невырожденным преобразованием переменных, то ранг квадратичной формы равен рангу матрицы квадратичной формы, т.е. равен числу ненулевых коэффициентов в форме канонического вида.
Теорема 3. Число положительных и число отрицательных коэффициентов в форме канонического вида (сигнатура квадратичной формы) не зависит от способа приведения квадратичной формы к каноническому виду.
Доказательство. Допустим, что квадратичная форма f ранга r от n переменных двумя способами приведена к каноническому виду,
![]() , (1)
, (1)
где предполагаем, что все коэффициенты сi и di (i=1,…,n) положительны. Пусть исходные переменные связаны с новыми переменными посредством невырожденных преобразований:
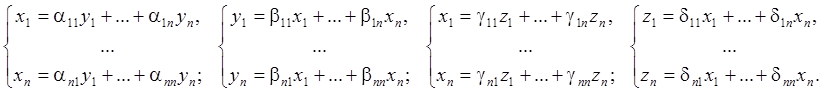
Допустим, что число положительных коэффициентов в канонических формах неодинаково. Пусть, для определенности, s < l. Положим
y1 =0,…, ys = 0, zs+1 =0, …, zn =0, (2)
и рассмотрим эти s + n - l равенств. Все эти yi и zj являются линейными формами от x1, …, xn . Таким образом, написанная совокупность равенств есть система однородных линейных уравнений относительно x1, …, xn. Число неизвестных равно n, число уравнений равно s + n - l< n. Поэтому система имеет нетривиальное (ненулевое) решение. Пусть x1*,…, xn*-одно из них Соответствующие значения для y1, …, ynобозначим через y1*, …, yn*. По условию (2) y1* =0,…, ys* = 0. Соответствующие значения для z1,…, zn обозначим через z1*,…, zn*. Они не все равны нулю, иначе все x1*, …, xn* равнялись бы нулю. Таким образом, среди чисел z1*,…, zn*есть отличные от нуля, но zs+1* =0, …, zn* =0.
Из представлений (1) в силу указанного выбора значений переменных находим
![]() .
.
Мы пришли к противоречию и наше предположение неверно. Следовательно, s = l.
Пример
1. Квадратичная форма ![]() в силу примера 3.1
имеет ранг 3, сигнатуру (1, 2).
в силу примера 3.1
имеет ранг 3, сигнатуру (1, 2).
5. Приведение квадратичной формы к каноническому виду по методу собственных значений.
Определение 1. Самосопряженный линейный оператор A в евклидовом пространстве En называется присоединенным к квадратичной форме f(x), если
f(x) = (x, Ax). (1)
Теорема 1. Если квадратичная форма имеет присоединенный линейный оператор, то в любом ортонормированном базисе его матрица равна матрице квадратичной формы.
Доказательство. В ортонормированном базисе, соотношение (1) запишется в виде X t B X = X tA X, где A - матрица оператора A, B - матрица квадратичной формы, X - координатный столбец вектора x. Это равенство можно записать в виде
X t (B-A) X = 0. (2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.