Математика \ Алгебра и геометрия

Билинейные и квадратичные формы. Приведение квадратичной формы к каноническому виду. Метод Лагранжа, страница 2

f(x)=XtBX ,                                                                                      (2)

f(x)= .                                                                               (3)

Доказательство.  Матричная запись квадратичной формы следует из теоремы 1 § 1. Представление квадратичной формы в виде однородного многочлена второй степени от координат x1, x2,…, xn вектора следует из определения произведения матриц (см. доказательство теоремы 1 § 1). 

Квадратичную форму (3) удобно записывать в виде f(x1, x2,…, xn). После приведения подобных членов в (3) квадратичную форму f(x)  удобно представить также в виде

f(x1, x2,…, xn) =                                                            (4)

Пример 1. Функция h(x, y) = 2x1 y1- x2 y2 + x2y1+ x1 y2 , где x = (x1, x2),  y= (y1, y2)ÎR2, симметричная билинейная форма на R2, которая имеет матрицу

.

Ей соответствует квадратичная форма  f(x1, x2) = f(x) = h(x, x) = 2x12- x22+ 2x1x2, матрица которой совпадает с указанной выше матрицей, и f(x1, x2) можно записать в матричном виде:

f(x1, x2) =.

Пусть v = (v1, v2,…, vn), u = (u1, u2,…, un) - два базиса векторного пространства V, T- матрица перехода от базиса v к базису u. Пусть B = (bij)n´n и С = (сij)n´n - матрицы квадратичной формы f(x) соответственно относительно базисов v и u, X, Y - координатные столбцы вектора x относительно базисов v и u. Тогдапо теореме 2 § 1

С = TtBT.                                                                                               (5)

По формулам преобразования координат X=TY. Тогда квадратичную форму  f(x)=XtBX можно записать в виде

f(x)= (TY)tB(TY) = Yt(TtBT)Y = YtСY = h(y1, y2,…, yn).                                                                  (6)

где Y = (y1, y2,…, yn)t .

Можно рассмотреть любое линейное преобразование переменных  y1, y2,…, yn в x1, x2,…, xn по формулам:

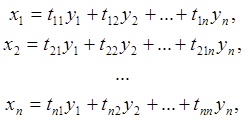                                                                        (7)

которое можно сокращенно представить в виде

X=TY,                                                                                                 (7) где X = (x1, x2,…, xn)t, Y = (y1, y2,…, yn)t.

По доказанному выше получаем теорему

Теорема 2. При линейном преобразовании переменных (7) квадратичная форма f(x1, x2,…, xn)=XtBX  переходит в квадратичную форму  h(y1, y2,…, yn) = YtСY, где С = TtBT . 

Если det T = 0, то преобразование (7) называется вырожденным. Если det T ¹ 0, то преобразование (7) называется невырожденным. Для невырожденного преобразования неизвестных существует обратное преобразование переменных x1, x2,…, xn в  y1, y2,…, yn по формуле:

Y =T -1 X.(8)

3.  Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции.

Теорема 1. Любую квадратичную форму

f(x1, x2,…, xn) = f(x)= .                                                                     (1)

 невырожденным линейным преобразованием X=TY, где X = (x1, x2,…, xn)t, Y = (y1, y2,…, yn)t, можно привести к виду

h(y1, y2,…, yn) = .                                                                            (2)

Представление квадратичной формы в виде (2) называется каноническим видом квадратичной формы. Коэффициенты называются каноническими коэффициентами. Матрица квадратичной формы канонического вида - диагональная матрица.

Доказательство.  Докажем теорему методом математической индукции по числу n переменных в квадратичной форме f. Пусть n =1. Тогда квадратичная форма f имеет вид  f  = b11x12 и является квадратичной формой канонического вида.  

Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем n переменных, и докажем ее для квадратичной формы  f, имеющей n переменных.  Рассмотрим два случая.

1. Среди диагональных коэффициентов b11, b22, …, bnn есть отличный от нуля. Пусть, например, b11 ¹ 0. Рассмотрим квадратичную форму , которая содержит такие же члены с неизвестным , как и наша форма f. Тогда разность

f(x1, x2,…, xn) - 

будет квадратичной формой, содержащей только неизвестные x2,…, xn. Отсюда

.

Вводим неизвестные

,                                                   (3)

и получим

,                                                               (4)

Скачать файл